什么是“好”？机器学习模型的准确性？

在机器学习中使用分类模型时，我们经常用来评估模型质量的一项指标是准确性。

精度只是模型正确分类的所有观测值的百分比。

计算方法如下：

准确度 = (# 真阳性 + # 真阴性) / (总样本量)

学生经常问的关于准确性的问题是：

什么被认为是机器学习模型准确性的“良好”值？

尽管模型的准确度可能在 0% 到 100% 之间变化，但我们没有用来确定模型是否具有“良好”准确度的通用阈值。

相反，我们通常将模型的准确性与参考模型的准确性进行比较。

基线模型只是预测数据集中的每个观察结果属于最常见的类别。

在实践中，任何比参考模型精度更高的分类模型都可以被认为是“有用的”，但显然我们的模型和参考模型之间的精度差异越大越好。

下面的示例展示了如何粗略地确定分类模型是否具有“良好”的准确性。

示例：确定模型是否具有“良好”的准确性

假设我们使用逻辑回归模型来预测 400 名不同的大学篮球运动员是否会被选入 NBA。

以下混淆矩阵总结了模型所做的预测：

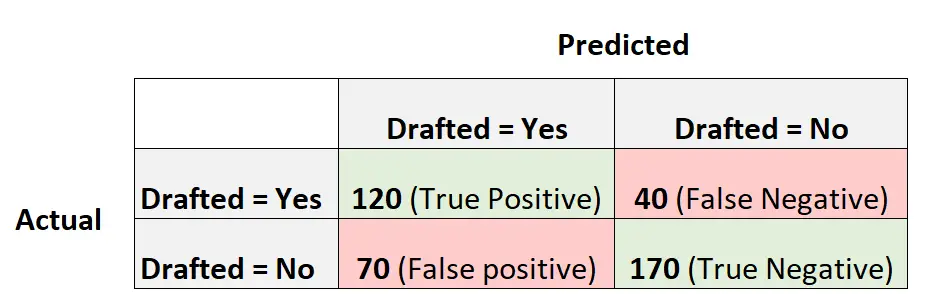
以下是计算该模型精度的方法：

• 准确度 = (# 真阳性 + # 真阴性) / (总样本量)
• 准确度 = (120 + 170) / (400)
• 准确度 = 0.725

该模型正确预测了72.5%玩家的结果。

为了了解准确性是否“好”，我们可以计算基线模型的准确性。

在这个例子中，球员最常见的结果是落选。具体来说，400 名球员中有 240 人落选。

一个基本模型是简单地预测每个球员都会落选的模型。

该模型的准确度计算如下：

• 准确度 = (# 真阳性 + # 真阴性) / (总样本量)
• 准确度 = (0 + 240) / (400)
• 准确度 = 0.6

这个基本模型可以正确预测60%玩家的结果。

在这种情况下，我们的逻辑回归模型在准确性方面比基线模型有了显着的提高，因此我们认为我们的模型至少是“有用的”。

在实践中，我们可能会拟合几种不同的分类模型，并选择最终模型作为与基线模型相比提供最大准确度增益的模型。

使用准确率评估模型性能的注意事项

精度是一种常用的指标，因为它很容易解释。

例如，如果我们说一个模型的准确率是 90%，我们就知道它正确分类了 90% 的观测值。

然而，准确性并没有考虑数据的分布方式。

例如，我们假设 90% 的球员没有被选入 NBA。如果我们有一个模型简单地预测每个球员都会落选，那么该模型将正确预测 90% 球员的结果。

这个值看起来很高，但模型实际上无法正确预测哪些球员将被选中。

经常使用的替代指标称为F1 Score ，它考虑了数据的分布方式。

例如，如果数据高度不平衡（例如，90% 的球员落选，10% 落选），那么 F1 分数将为模型的性能提供更好的评估。

在此处详细了解准确度和 F1 分数之间的差异。

其他资源

以下教程提供有关机器学习分类模型中使用的指标的更多信息：

什么是平衡精度？
什么被认为是“良好”的 F1 分数？