如何解释优势比

在统计学中，概率是指事件发生的可能性。计算方法如下：

可能性：

P(事件) = (# 理想的结果) / (# 可能的结果)

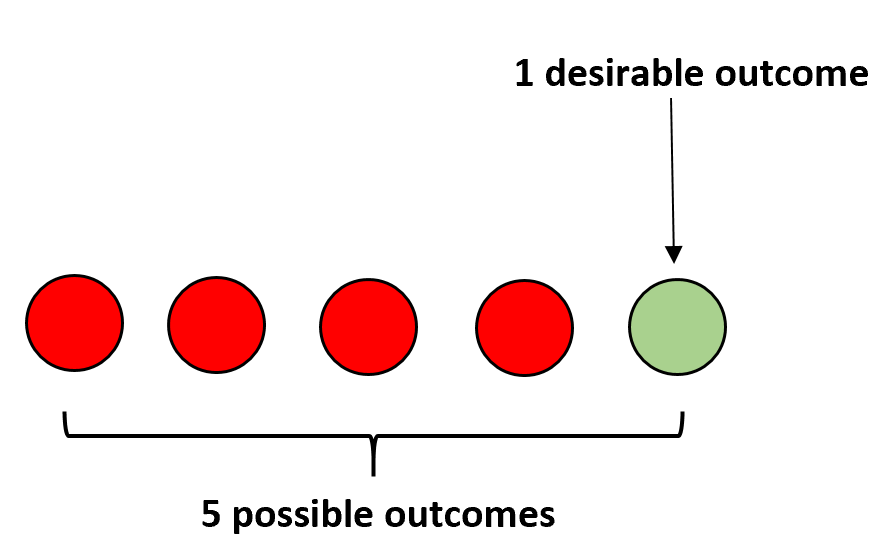
例如，假设袋子里有四个红球和一个绿球。如果闭上眼睛随机选择一个球，则选择绿色球的概率计算如下：

P（绿色）= 1 / 5 = 0.2 。

事件发生的概率可以计算如下：

赔率：

机会（事件）= P（事件发生）/ 1-P（事件发生）

例如，射出绿球的几率为 (0.2)/1-(0.2) = 0.2/0.8 = 0.25 。

优势比是两个概率的比值。

幸运报告：

赔率=事件A的赔率/事件B的赔率

例如，我们可以计算选择红球和绿球之间的优势比。

抽到红球的概率是 4/5 = 0.8 。

抽到红球的机会是 (0.8) / 1-(0.8) = 0.8 / 0.2 = 4 。

选择红球而不是绿球的优势比计算如下：

赔率（红色）/赔率（绿色）= 4 / 0.25 = 16 。

因此射出红球的机会是射出绿球的机会的 16 倍。

现实世界中何时使用优势比？

在现实世界中，优势比用于多种情况，研究人员希望比较两个事件发生的几率。这里有些例子。

示例#1：解释优势比

研究人员想知道与现有治疗相比，新治疗是否可以提高患者获得积极健康结果的机会。下表显示了根据治疗情况出现积极或消极健康结果的患者人数。

患者通过新治疗获得积极结果的机会可以计算如下：

机会= P(正) / 1 – P(正) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1.25

患者通过现有治疗获得积极结果的机会可以计算如下：

机会= P(正) / 1 – P(正) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0.875

因此，与现有治疗相比，新治疗取得积极结果的优势比可计算如下：

优势比= 1.25 / 0.875 = 1.428 。

我们将此解释为患者使用新治疗获得积极结果的几率是患者使用现有治疗获得积极结果的几率的1.428倍。

换句话说，新疗法获得阳性结果的几率增加了42.8% 。

示例#2：解释优势比

营销人员想知道一则广告是否比另一则广告更能让客户购买特定商品。因此他们向 100 人展示每个广告。下表显示了根据所看到的广告购买该商品的人数：

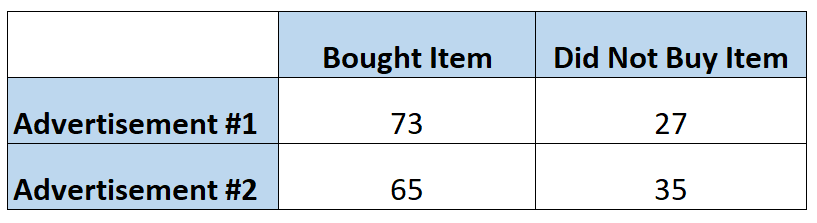
个人在看到第一个广告后购买该商品的机会可以计算如下：

赔率= P（买入）/ 1 – P（买入）= (73/100) / 1-(73/100) = (73/100) / (27/100) = 2.704

个人在看到第二个广告后购买该商品的机会可以计算如下：

赔率= P（买入）/ 1 – P（买入）= (65/100) / 1-(65/10) = (65/100) / (35/100) = 1.857

因此，客户在看到第一个广告后购买商品与在看到第二个广告后购买商品的优势比可计算如下：

优势比= 2.704 / 1.857 = 1.456 。

我们将此解释为个人在看到第一个广告后购买该商品的几率是个人在看到第二个广告后购买该商品的几率的1.456倍。

换句话说，由于首次上架，购买该商品的机会增加了45.6% 。

其他资源

如何在 Excel 中计算优势比和相对风险
如何解释比值比小于 1
如何解释相对风险