负二项式与泊松：如何选择回归模型

负二项式回归和泊松回归是当响应变量由离散计数结果表示时应使用的两种回归模型。

以下是代表离散计数结果的响应变量的一些示例：

• 从某个课程毕业的学生人数
• 某个路口发生交通事故的数量
• 完成马拉松比赛的人数
• 零售店指定月份的退货数量

如果方差近似等于平均值，则泊松回归模型通常可以很好地拟合数据集。

但是，如果方差显着大于平均值，则负二项式回归模型通常能够更好地拟合数据。

我们可以使用两种技术来确定泊松回归还是负二项式回归更适合给定的数据集：

1.残差图

我们可以根据回归模型的预测值创建标准化残差图。

如果大多数标准化残差在 -2 和 2 之间，则泊松回归模型可能是合适的。

但是，如果许多残差超出此范围，负二项式回归模型可能会提供更好的拟合。

2.似然比检验

我们可以将泊松回归模型和负二项式回归模型拟合到同一数据集，然后进行似然比检验。

如果检验的 p 值低于一定的显着性水平（例如 0.05），那么我们可以得出结论，负二项式回归模型提供了明显更好的拟合。

以下示例演示如何在 R 中使用这两种技术来确定对于给定数据集是使用泊松回归模型还是负二项式回归模型更好。

示例：负二项式回归与泊松回归

假设我们想知道给定县的一名高中棒球运动员根据他的学区（“A”、“B”或“C”）和他的学校成绩获得了多少奖学金。大学入学考试（从0到100测量）。 ）。

使用以下步骤确定负二项式回归模型还是泊松回归模型是否能更好地拟合数据。

第 1 步：创建数据

以下代码创建我们将使用的数据集，其中包括 1,000 名棒球运动员的数据：

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

步骤 2：拟合泊松回归模型和负二项式回归模型

以下代码显示如何将泊松回归模型和负二项式回归模型拟合到数据：

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

第 3 步：创建残差图

以下代码显示了如何为两个模型生成残差图。

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

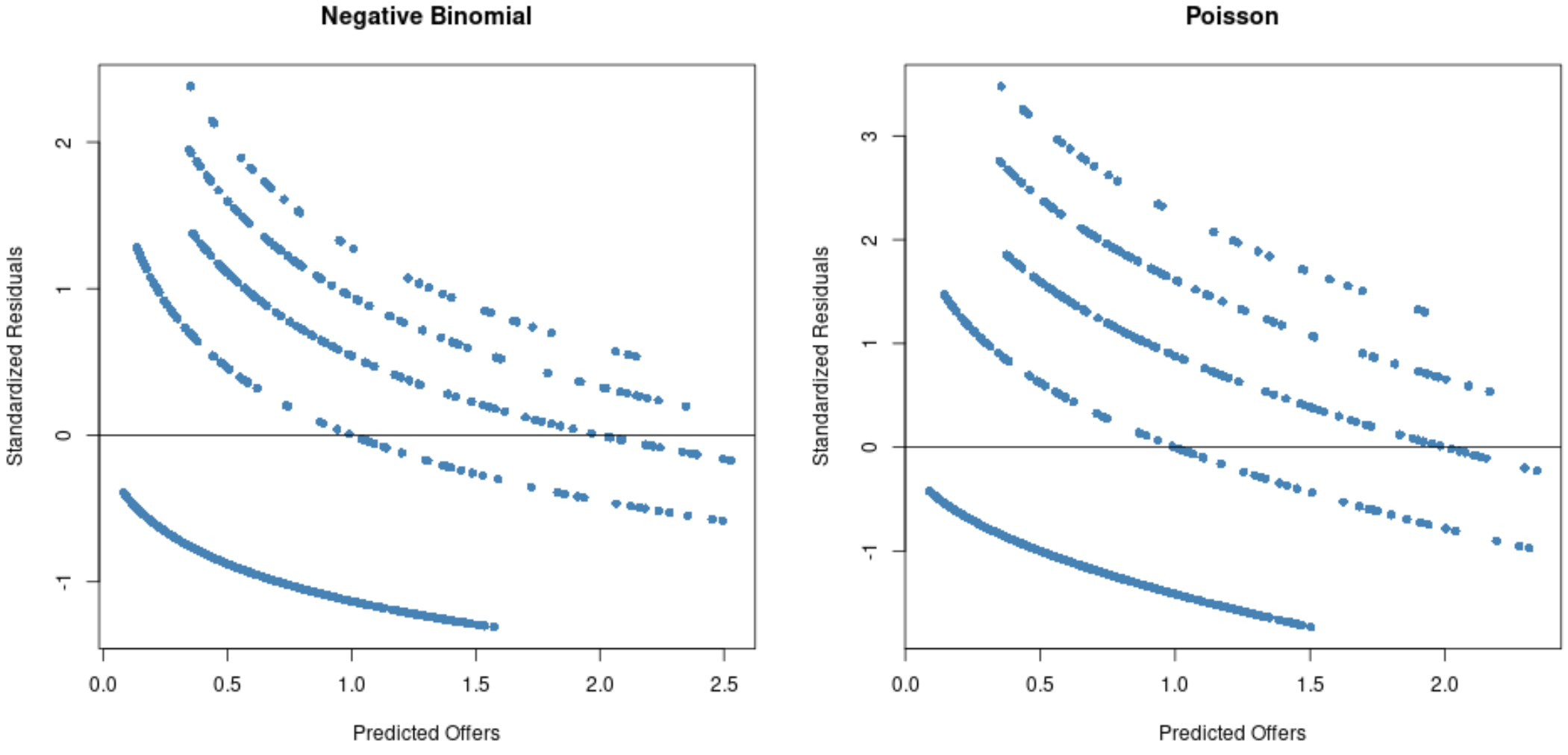
从图中我们可以看到，与负二项式回归模型相比，泊松回归模型的残差分布得更广（请注意，有些残差超出了 3）。

这表明负二项式回归模型可能更合适，因为该模型的残差较小。

步骤 4：执行似然比检验

最后，我们可以进行似然比检验来确定两个回归模型的拟合是否存在统计上显着的差异：

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

测试的 p 值为3.508072e-29 ，明显小于 0.05。

因此，我们可以得出结论，与泊松回归模型相比，负二项式回归模型对数据的拟合效果明显更好。

其他资源

负二项分布简介
泊松分布简介