什么是布兰德-奥特曼情节？ （定义&#038；示例）

Bland-Altman 图用于可视化两种不同仪器或两种不同测量技术之间的测量差异。

它通常用于评估用于测量某物的新仪器或技术与当前使用的仪器或技术的相似性。

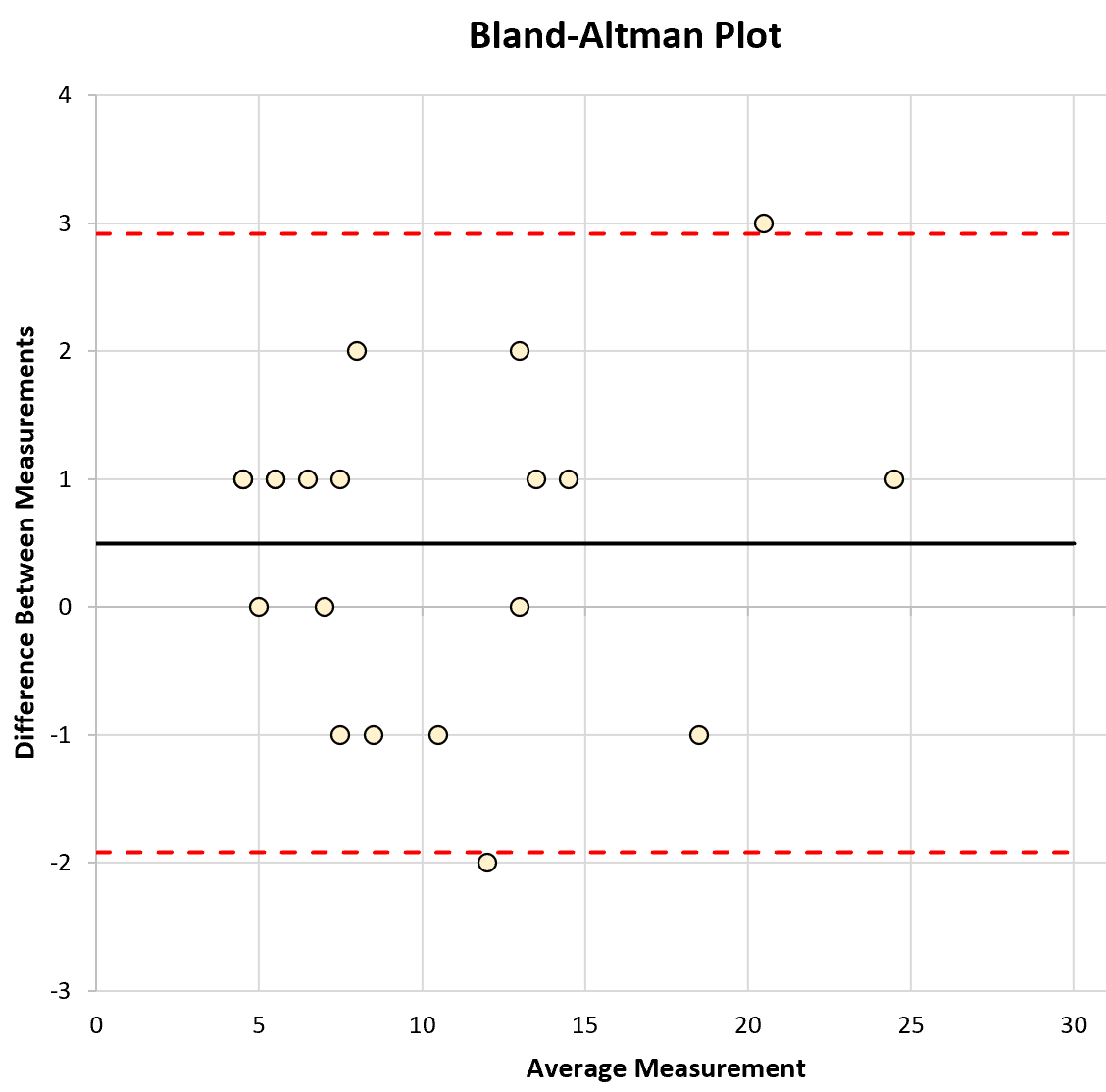
绘图的 x 轴显示两台仪器的平均测量值，y 轴显示两台仪器之间的测量值差异。

图中还显示了以下三行：

• 两台仪器测量结果的平均差异
• 均值差的 95% 置信区间上限
• 均值差的 95% 置信区间下限

这种类型的图对于确定两件事很有用：

1. 两台仪器测量结果的平均差异是多少？

图表中间绘制的水平线显示了两台仪器之间测量值的平均差异。该值通常称为仪器之间的“偏差”。

该值距离零越远，仪器之间测量的平均差异就越大。

2. 两种仪器之间的典型一致性范围是多少？

置信区间上限线和下限线让我们了解两种工具之间的典型一致性范围。一般来说，两种工具之间 95% 的差异都在这些置信限度内。

置信区间越宽，两种仪器之间的测量差异范围就越大。

以下分步示例展示了如何从头开始创建和解释 Bland-Altman 图。

注意： Bland-Altman 图有时称为 Tukey 均差图。这些名称可以互换使用。

第 1 步：收集数据

假设一位生物学家想知道两种不同的测量青蛙重量（以克为单位）的仪器有多相似。他使用两台仪器（A 和 B）对同一组 20 只青蛙进行称重。

各仪器测量的青蛙重量如下表所示：

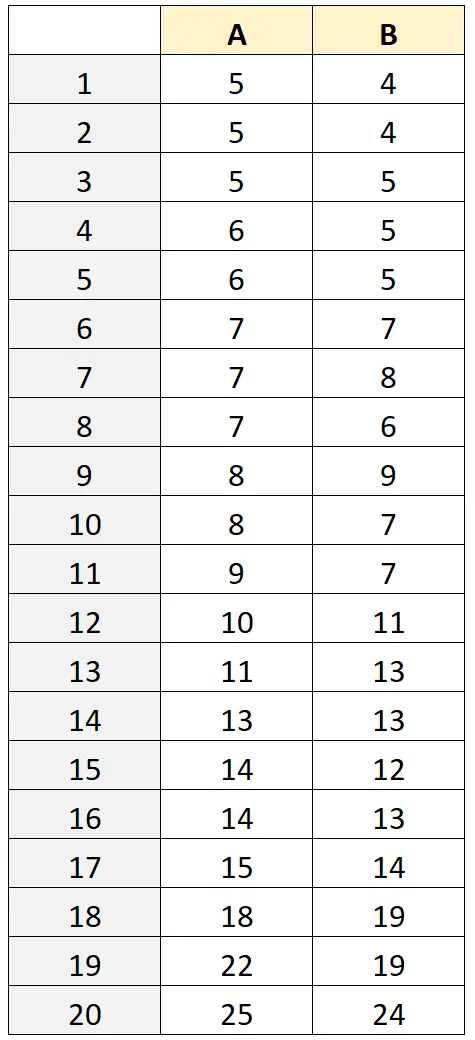
步骤 2：计算平均测量值和测量值差异

接下来，我们将计算每只青蛙的平均测量值 ((A+B)/2) 和测量值差 (AB)：

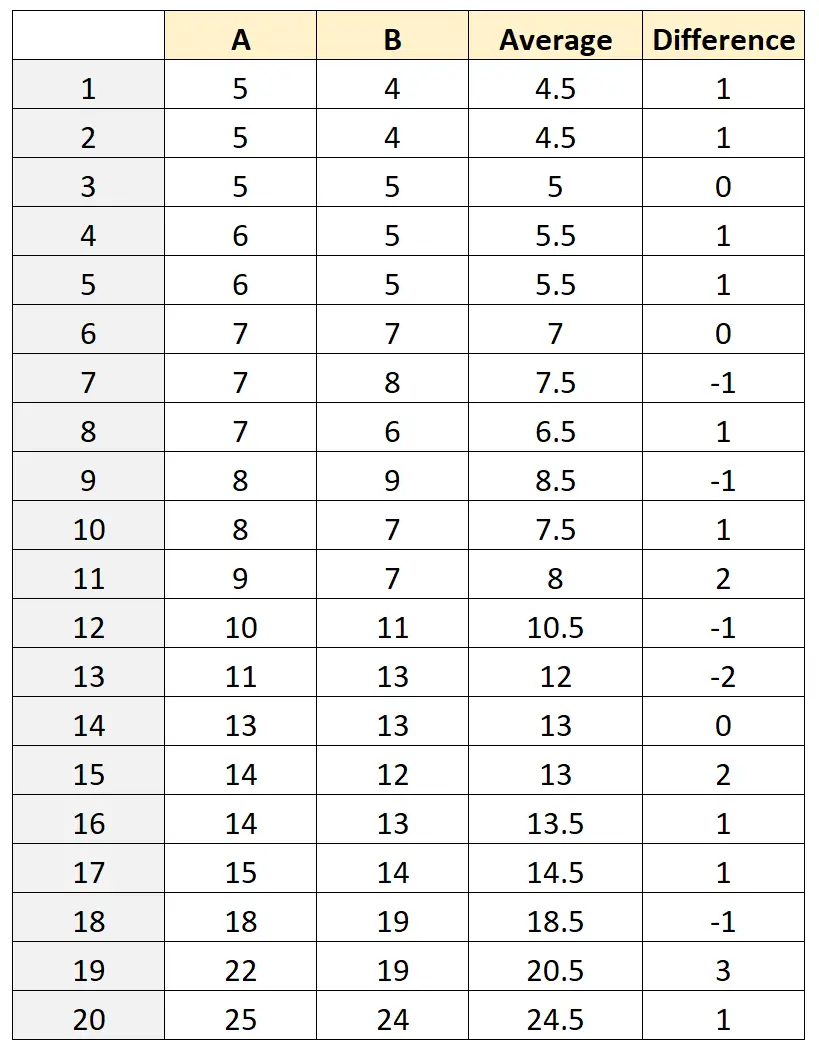
步骤 3：计算均值差和置信区间

差异列中值的平均值为0.5 。

差异列中值的标准差为1.235 。

均值差置信区间的上限和下限可以计算如下：

上限： x +1.96*s=0.5+1.96*1.235= 2.92

下限： x – 1.96*s = 0.5 – 1.96*1.235 = -1.92

以下是如何解释这些值：

• 平均而言，仪器 A 比仪器 B 重 0.5 克。
• 两台仪器之间95%的重量差异应在-1.92克到2.92克之间。

接下来，我们将创建一个 Bland-Altman 图来可视化这些值。

第 4 步：创建绘图

然后我们可以创建以下图，在 x 轴上显示两台仪器的平均测量值，在 y 轴上显示测量值之间的差异。

我们还可以向测量值之间的平均差 (0.5) 添加一条水平线，以及我们在上一步中计算的置信上限 (2.92) 和置信下限 (-1.92)：

其他资源

如何在 Excel 中创建平淡奥特曼图
如何在 R 中创建 Bland-Altman 图
如何用 Python 创建 Bland-Altman 图