逻辑回归
本文解释了统计学中的逻辑回归是什么。同样,您将找到逻辑回归公式、逻辑回归的不同类型以及已解决的逻辑回归练习。
什么是逻辑回归?
在统计学中,逻辑回归是一种用于预测分类变量结果的回归模型。也就是说,逻辑回归用于根据自变量对分类变量取特定值的概率进行建模。
最常见的逻辑回归模型是二元逻辑回归,其中只有两种可能的结果:“失败”或“成功”(伯努利分布)。 “失败”用值 0 表示,而“成功”用值 1 表示。
例如,可以使用逻辑回归模型来研究学生根据学习时间通过考试的概率。在这种情况下,失败将是“失败”的结果,而另一方面,成功将是“成功”的结果。
逻辑回归公式
逻辑回归模型的方程为:
![]()
因此,在逻辑回归模型中,获得“成功”结果,即因变量取值为1的概率,可以通过以下公式计算:
![]()
金子:
-

是因变量为 1 的概率。
-

是逻辑回归模型的常数。
-

是变量 i 的回归系数。
-

是变量 i 的值。
逻辑回归模型示例
现在我们知道了逻辑回归的定义,让我们看一个如何创建此类回归模型的具体示例。
- 下表汇总了 20 条数据,其中涉及每个学生的学习时间以及他们是否通过或未通过统计考试。运行逻辑回归模型并计算学生学习 4 小时后通过的概率。
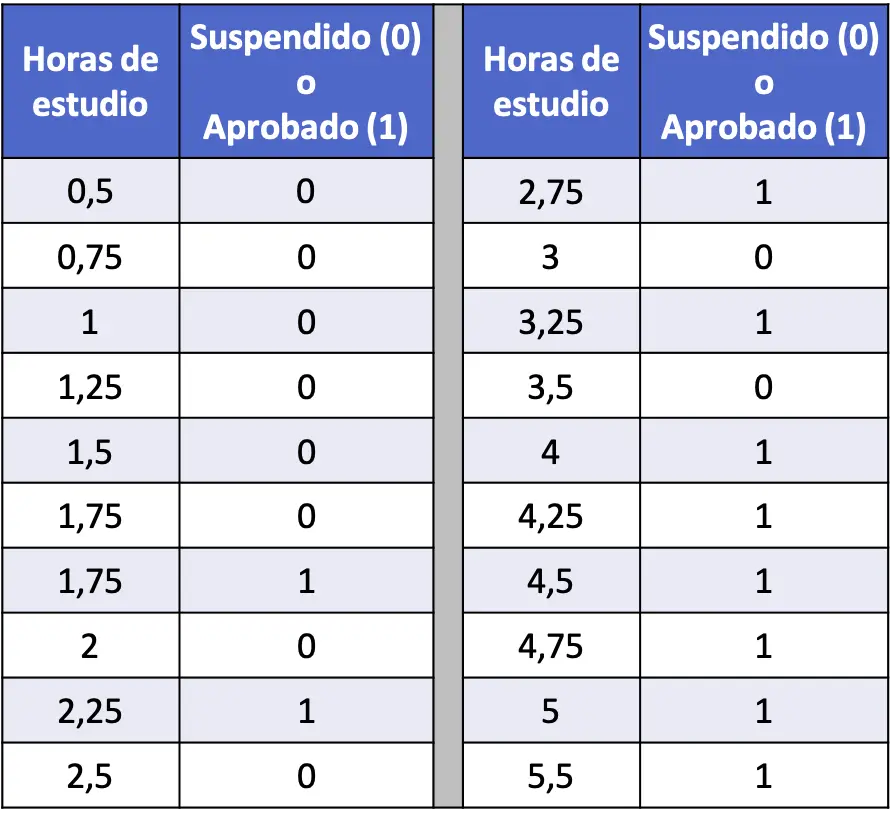
在本例中,解释变量是学习时数,响应变量是学生未通过 (0) 还是通过 (1)。因此,在我们的模型中,我们只有系数
![]()
和系数
![]()
,因为只有一个自变量。
![]()
手动确定回归系数非常费力,因此建议使用Minitab等计算机软件。因此,使用Minitab计算出的回归系数的值如下:
![Rendered by QuickLaTeX.com \begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6ed66de602220c69aabb71a726fec9f8_l3.png)
因此逻辑回归模型如下:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0902ac67194bedf38d5f4ff06dc27a38_l3.png)
下面您可以看到绘制的样本数据和逻辑回归模型方程:
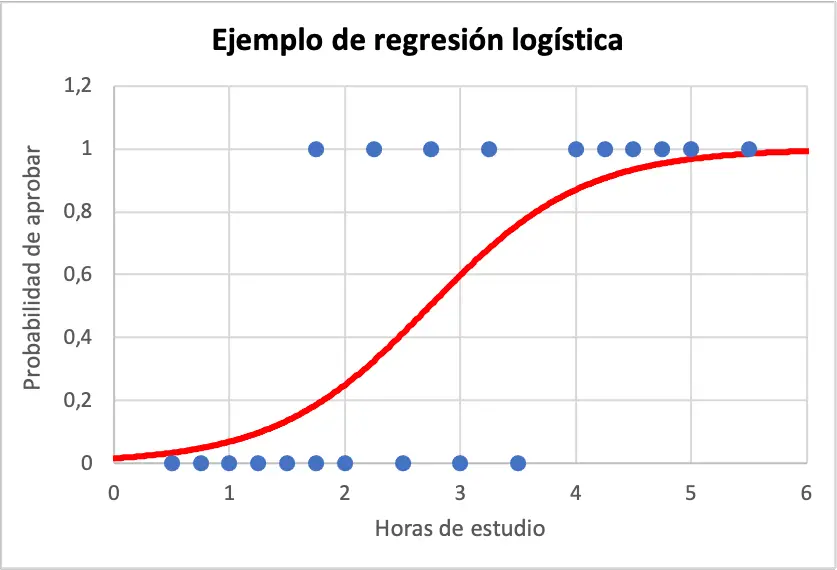
因此,要计算学生学习 4 小时后成功的概率,只需使用从逻辑回归模型获得的方程即可:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-930691eafee62c04e59d9c4de8ef6a76_l3.png)
简而言之,如果学生学习四个小时,他们通过考试的概率为 86.99%。
逻辑回归的类型
逻辑回归分为三种类型:
- 二元Logistic回归:因变量只能有两个值(0和1)。
- 多项式逻辑回归:因变量有两个以上的可能值。
- 序数逻辑回归:可能的结果具有自然顺序。
逻辑回归和线性回归
最后,总而言之,我们将了解逻辑回归和线性回归之间的区别,因为统计学中最常用的回归模型是线性模型。
线性回归用于对数值因变量进行建模。此外,在线性回归中,解释变量和响应变量之间的关系是线性的。
因此,逻辑回归和线性回归之间的主要区别在于因变量的类型。在逻辑回归中,因变量是分类变量,而线性回归中的因变量是数值变量。
因此,逻辑回归用于预测两个可能选项之间的结果,而线性回归有助于预测数值结果。