省略变量偏差：定义和示例

当回归模型中不包含相关解释变量时，就会出现遗漏变量偏差，这可能会导致模型中一个或多个解释变量的系数出现偏差。

由于以下两个原因之一，遗漏变量通常会被排除在回归模型之外：

1.变量的数据根本不可用。

2.解释变量对响应变量的影响未知。

为了让遗漏变量真正扭曲模型系数，必须满足以下两个条件：

1.省略的变量必须与模型中的一个或多个解释变量相关。

2.省略的变量必须与模型中的响应变量相关。

遗漏变量偏差的影响

假设我们有两个解释变量 A 和 B，以及一个响应变量 Y。假设我们拟合一个简单的线性回归模型，其中 A 作为唯一的解释变量，并将 B 排除在模型之外。

如果 B 与 A 相关并且与 Y 相关，这将导致 A 的系数估计出现偏差。下图显示了 A 的系数估计将如何出现偏差，具体取决于与乙：

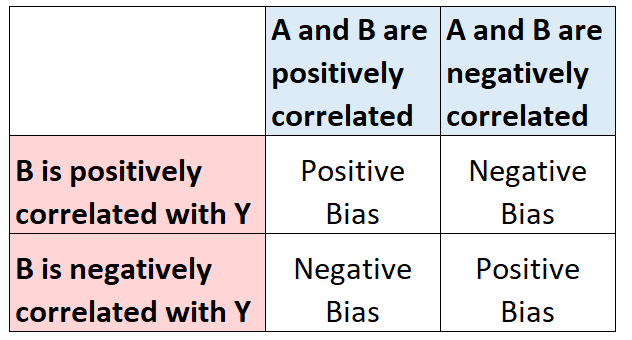
示例：省略变量偏差

假设我们要研究平方英尺对房地产价格的影响，因此我们应用以下简单线性回归模型：

房价=B ₀ + B ₁ （平方面积）

假设我们发现估计模型是：

房价=40203.91+118.31（平方面积）

我们解释平方英尺系数的方式是，平方英尺每增加一单位，房价平均就会上涨 118.31 美元。

然而，假设我们忽略了解释变量年龄，它与平方英尺呈强烈负相关，并与房地产价格呈强烈负相关。该变量应该在模型中，但事实并非如此。因此，平方英尺的系数估计可能有偏差。

由于年龄与模型中的解释变量和响应变量均呈负相关，因此我们预计平方英尺的系数估计值会出现正偏差：

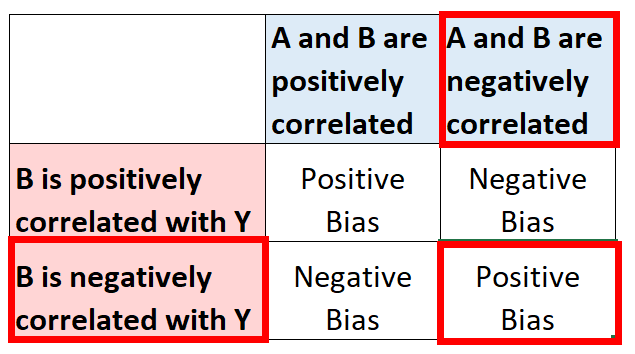
假设我们找到有关住宅年龄的数据，然后将其包含在模型中。模型则变为：

房价=B ₀ + B ₁ （面积）+B ₂ （年龄）

假设我们发现估计模型是：

房价 = 123,426.20 + 81.06（面积） – 1,291.04（年龄）

请注意，平方英尺的系数估计值已显着下降，这意味着它在之前的模型中存在正偏差。

我们在此模型中解释平方英尺系数的方式是，假设房龄保持不变，平方英尺每增加一单位，平均房价就会增加 81.06 美元。

关于遗漏变量偏差该怎么办

不幸的是，遗漏变量偏差经常发生在现实世界中，因为某些变量通常应该包含在回归模型中，但由于它们的数据不可用或者它们与响应变量之间的关系未知而没有包含在回归模型中。

如果可能，您应该尝试在回归模型中包含所有相关的解释变量，以便您能够了解解释变量与响应变量之间的真实关系。

从模型中排除相关解释变量可能会显着影响模型的解释，正如我们在前面的房地产价格示例中看到的那样。

其他资源

什么是隐藏变量？
什么是令人困惑的变量？