三角分布简介
三角分布是具有三角形概率密度函数的连续概率分布。
它由三个值定义:
- 最小值有
- 最大值b
- 最大值c
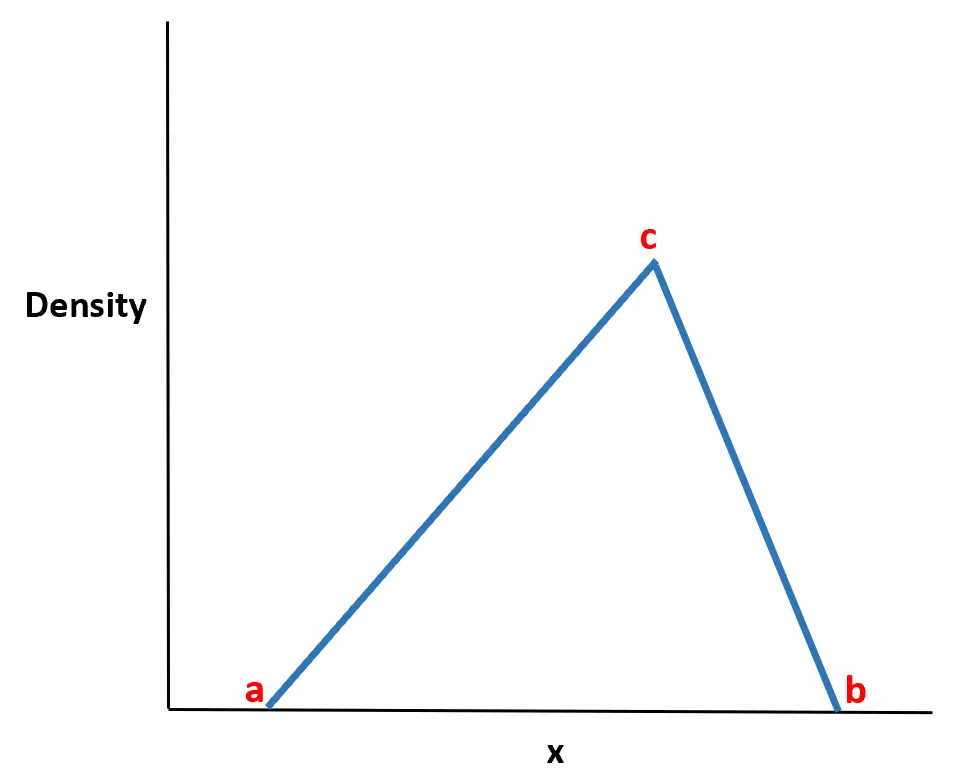
该分布的名称来源于概率密度函数具有三角形形状的事实。
事实证明,这种分布在现实世界中非常有用,因为我们通常可以估计随机变量将采用的最小值 (a)、最大值 (b) 和最可能的值 (c)。通常可以使用仅知道这三个值的三角分布来对随机变量的行为进行建模。
例如,一家餐厅可能估计下周的总销售额最低为 10,000 美元,最高为 30,000 美元,最有可能为 25,000 美元。

仅使用这三个数字,他们就可以使用三角分布来确定进行一定数量销售的概率。
三角分布的性质
三角分布具有以下性质:
PDF:
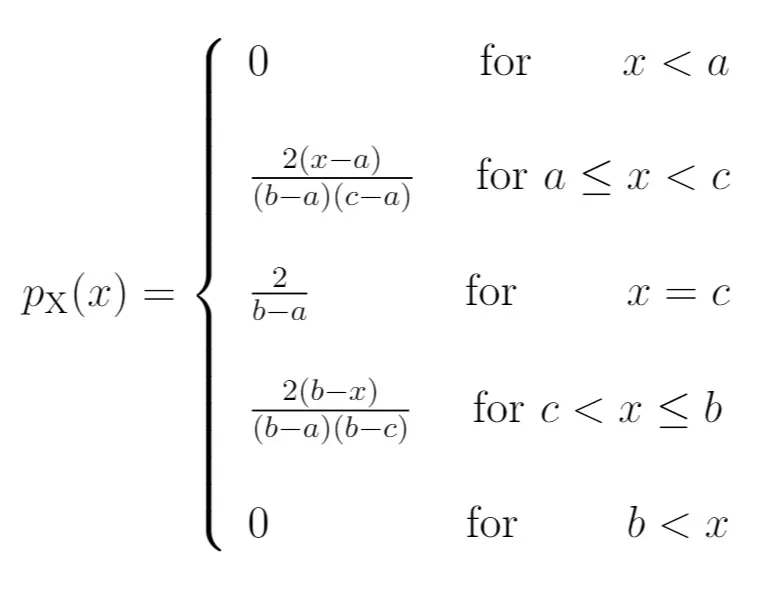
累积分布函数:
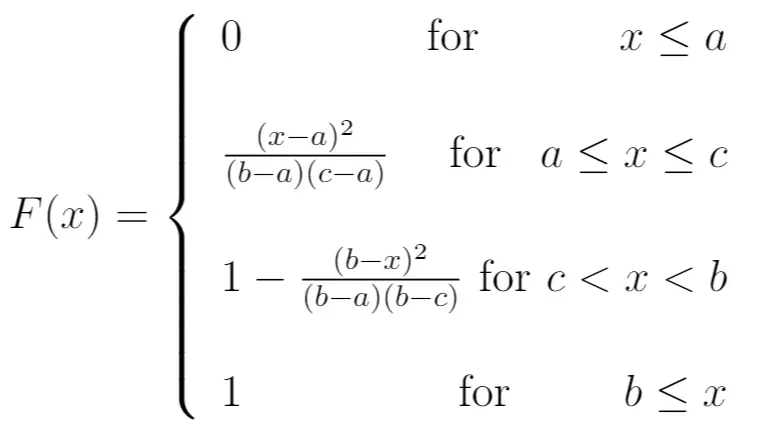
平均值: (a + b + c) / 3
模式: c
方差: (a 2 + b 2 + c 2 – ab – ac – bc) / 18
使用三角分布的示例
让我们回到前面的例子。假设一家餐厅估计其下周的总销售额最低为 10,000 美元,最高为 30,000 美元,最有可能为 25,000 美元。

该餐厅总销售额低于 20,000 美元的概率是多少?
为了回答这个问题,我们可以问 x = 总销售额。我们知道 x 位于最小值a 10,000 美元和最大值c 25,000 美元之间。
因此,根据 PDF,我们可以使用以下等式求出餐厅总销售额低于 20,000 美元的概率:
- P(X < $20,000) = (xa) 2 / ((ba)(ca))
- P(X < $20,000) = (20,000-10,000) 2 / ((30,000-10,000)(25,000-10,000))
- P(X < 20,000 美元) = 0.333
餐厅总销售额低于 20,000 美元的概率为0.333 。
餐厅的平均预期销售额是多少?
我们可以使用前面给出的平均值公式计算预期平均销售额:
- 平均值 = (a + b + c) / 3
- 平均值 = ($10,000 + $30,000 + $25,000) / 3
- 平均 = $21,667
平均预期销量为21,667 辆。
其他资源
以下教程提供了其他常用发行版的介绍: