什么是不相交事件？ （定义和示例）

不相交事件是不能同时发生的事件。

用概率符号表示，如果事件A和B的交集为零，则它们是不相交的。这可以写成如下：

• P(A 和 B) = 0
• P(A∩B) = 0

例如，假设我们从一副牌中随机选择一张牌。设事件 A 为牌为黑桃或梅花的事件，设事件 B 为牌为红心或方块的事件。

我们将事件的样本空间定义如下：

• A = {黑桃, 梅花}
• B = {心形，钻石}

请注意，两个采样空间之间没有重叠。因此，事件 A 和 B 是不相交事件，因为它们不能同时发生。

注意：不相交事件也称为互斥事件。

不相交事件的示例

以下是一些不相交事件的更多示例。

示例1：绘制

假设你抛一枚硬币。设事件 A 为硬币落在正面的事件，事件 B 为硬币落在正面的事件。

事件 A 和事件 B 是不相交的，因为它们不能同时发生。硬币不能正面或反面落地。

示例2：掷骰子

假设你掷骰子。设事件 A 为骰子落在奇数上的事件，设事件 B 为骰子落在偶数上的事件。

事件 A 和事件 B 是不相交的，因为它们不能同时发生。骰子不能落在偶数和奇数上。

示例 3：职业碗位置

假设 NFL 要选择举办职业碗比赛的地点。他们缩小了迈阿密和圣地亚哥的选择范围。他们将两个名字放在帽子里，然后随机选择一个。我们假设事件 A 是他们选择迈阿密进行的事件，事件 B 是他们选择圣地亚哥进行的事件。

事件 A 和事件 B 是不相交的，因为它们不能同时发生。迈阿密和圣地亚哥都无法选择。

查看不相交的事件

可视化不相交事件的一个有用方法是创建维恩图。

如果两个事件不相交，它们在维恩图中根本不会重叠：

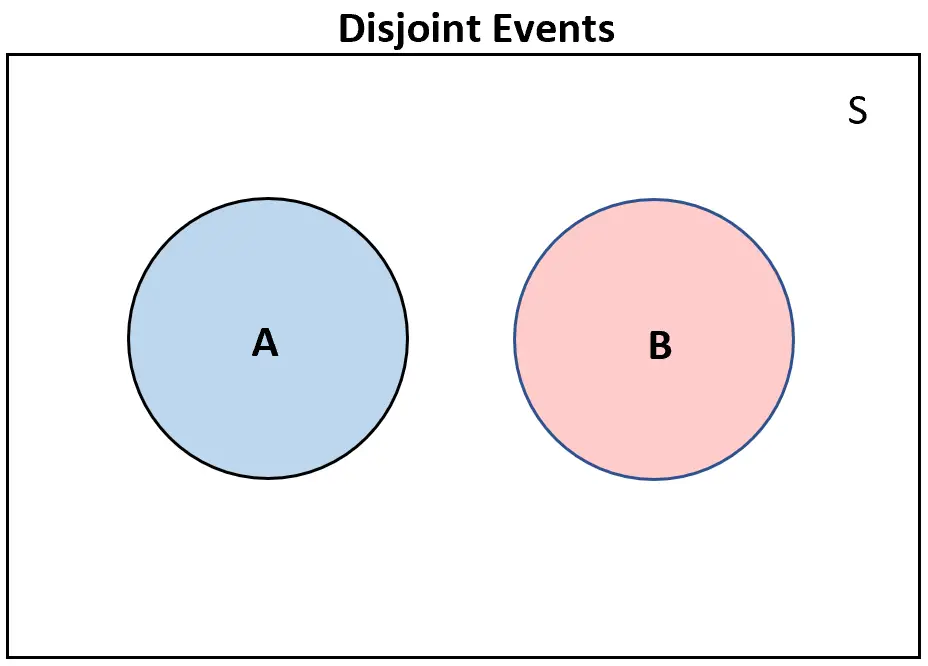
相反，如果两个事件不相交，则维恩图中至少会有一些重叠：

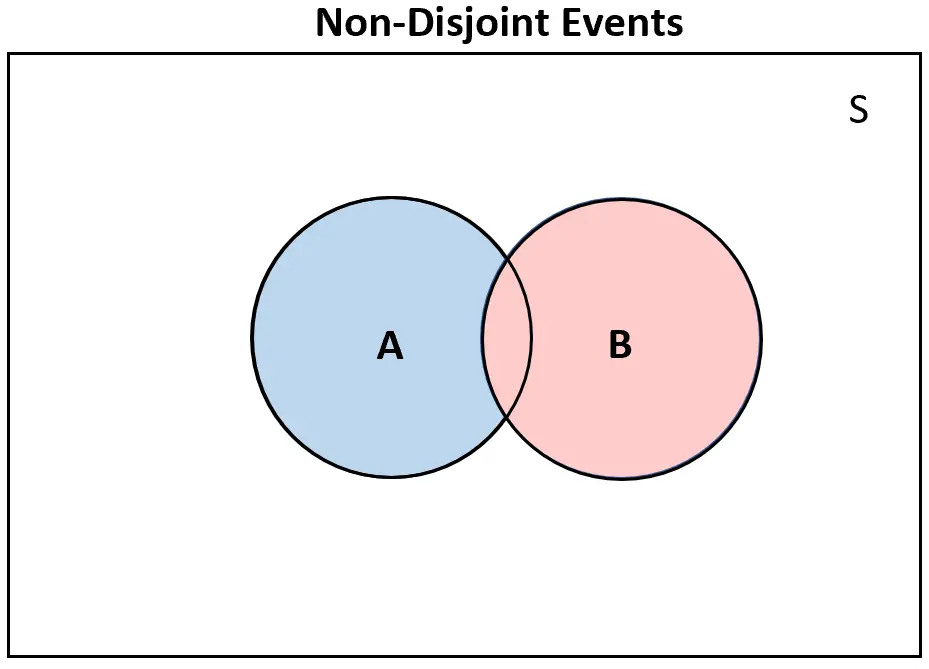
不相交事件的概率

正如前面提到的，如果两个事件不相交，那么它们同时发生的概率为零。

• P(A∩B) = 0

同样，任一事件发生的概率可以通过将它们各自的概率相加来计算。

• P(A∪B) = P(A) + P(B)

例如，让事件 A 为骰子落在 1 或 2 上的事件，让事件 B 为骰子落在 5 或 6 上的事件。

我们将事件的样本空间定义如下：

• A = {1, 2}
• B = {5, 6}

我们将事件 A 或事件 B 发生的概率计算为：

• P(A∪B) = P(A) + P(B)
• P(A∪B) = 2/6 + 2/6
• P(A∪B) = 4/6 = 2/3

事件A或事件B发生的概率是2/3 。

其他资源

以下教程提供了其他常见概率主题的说明：

如何求 A 或 B 的概率：举例
如何求 A 和 B 的概率：举例
全概率定律：定义和示例