根意味着平方

在这里我们解释什么是均方根以及它是如何计算的。此外，您还将了解使用平均值和逐步解决练习的优点和缺点。最后，您将能够使用本文末尾的计算器计算任何数据集的均方根。

什么是均方？

均方根是描述性统计中心性的度量。均方根等于数据平方算术平均值的平方根。

均方根也称为均方根或RMS 。

因此，二次均值的公式如下：

当统计变量取正值和负值时，均方特别有用，因为通过对每条数据进行平方，所有值都变为正值。因此，均方用于分析符号不重要但绝对值重要的变量。

例如，均方用于研究测量误差，因为在这些情况下我们不是看误差是正还是负，而是分析测量时误差的大小。

另外，大数字的平方比小数字的平方具有更高的值，因此在中间的正方形中大数字比小数字更重要。

平方平均是统计平均的一种，与算术平均、加权平均、几何平均、调和平均一样。

均方根的优点和缺点

与其他类型的平均值相比，二次平均值有优点和缺点。

二次均值的主要优点是它允许您获得离散变量平均值的非常好的近似值。另一方面，平方平均值的一大缺点是其计算相当复杂，因为必须进行多次运算。

相反，均方根对于分析误差测量非常有用。它还更加重视高值，尽管此属性意味着错误的测量将显着改变均方根结果。

如何计算均方根

要计算均方根，必须执行以下步骤：

1. 计算每个统计数据的平方。
2. 将上一步计算出的所有平方相加。
3. 将结果除以样本中数据项的数量。
4. 求前一个值的平方根。
5. 获得的结果是统计样本的平方平均值。

👉您可以使用下面的计算器来计算任何数据集的均方根。

均方例子

一旦我们知道如何获得均方根，我们将以确定一组数据的均方根为例。

• 在大学实验课上，教授要求学生做一个化学实验。化学实验的目标是获得总共3升的溶液。学生小组获得以下数据：

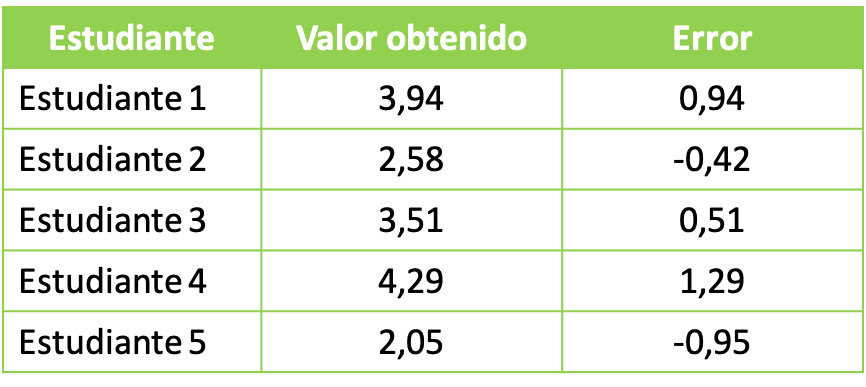
为了研究获得的统计数据，我们继续计算每组获得的误差的均方值。因此，我们应用二次平均公式：

我们将数据代入公式并计算均方根：

因此，根据均方根，实验中获得的平均误差为0.88升。

均方计算器

将任何统计样本的数据输入以下计算器以计算其均方根。数据必须用空格分隔，并使用句点作为小数点分隔符输入。