临界值
本文解释了统计学中的临界值是什么以及如何在假设检验中解释它。同样,您将能够看到如何计算临界值以及几个具体示例。
什么是临界值?
临界值是检验统计量分布中将原假设的拒绝区域与其接受区域分开的点。换句话说,临界值是统计检验的分布值,它标志着拒绝区域(或临界区域)的界限。
通常,临界值由符号 Z α/2表示,因为最常见的参考分布通常是标准正态分布。
一般来说,单边检验具有临界价值,因为拒绝区域构成了分布的单个尾部。另一方面,双尾检验有两个临界值,因为拒绝区域对应于分布的两个尾部。
在置信区间中,临界值是参考分布中标记置信区间界限的点。
如何计算临界值
然后我们将看到最常见的临界值是如何计算的。 Z的临界值和t的临界值是针对均值的置信区间计算的,唯一的区别是Z的临界值是在总体标准差已知的情况下计算的,而不是使用t的临界值当仅知道一个样本的数据时。
Z 的临界值
Z 的临界值用于确定平均值置信区间的极限。更准确地说,仅当您知道总体标准差时才使用它。
要计算Z的临界值,必须在标准正态分布表中找到与显着性水平一半的概率对应的值。
例如,如果我们想要确定置信水平为 95% 的平均值的置信区间,这意味着显着性水平为 5%。因此,有必要在标准正态分布表中查看哪个值对应于 2.5% 的概率,因为均值的置信区间是两侧的。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
您可以在下面看到包含最常用的临界 Z 值的表格:
| 置信度 (1-α) | 显着性水平 (α) | 临界值(Zα /2 ) |
|---|---|---|
| 0.80 | 0.20 | 1,282 人 |
| 0.85 | 0.15 | 1,440 |
| 0.90 | 0.10 | 1,645 |
| 0.95 | 0.05 | 1960年 |
| 0.99 | 0.01 | 2,576 |
| 0.995 | 0.005 | 2,807 |
| 0.999 | 0.001 | 3,291 |
t 的临界值
当总体标准差未知时,临界 t 值用于查找均值置信区间的极限。
为了计算 t 的临界值,必须在Student t 分布表中找到与显着性水平一半的概率相对应的值,同时考虑到 Student t 分布的自由度是一个单位。比样本大小。
例如,如果我们想要找到置信度为 95% 且样本量为 8 的置信区间,我们需要访问 Student t 分布表并查看哪个值对应于 t 0.025|7 。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-2caa8c4576ebc261acfdb1341dc4567d_l3.png)
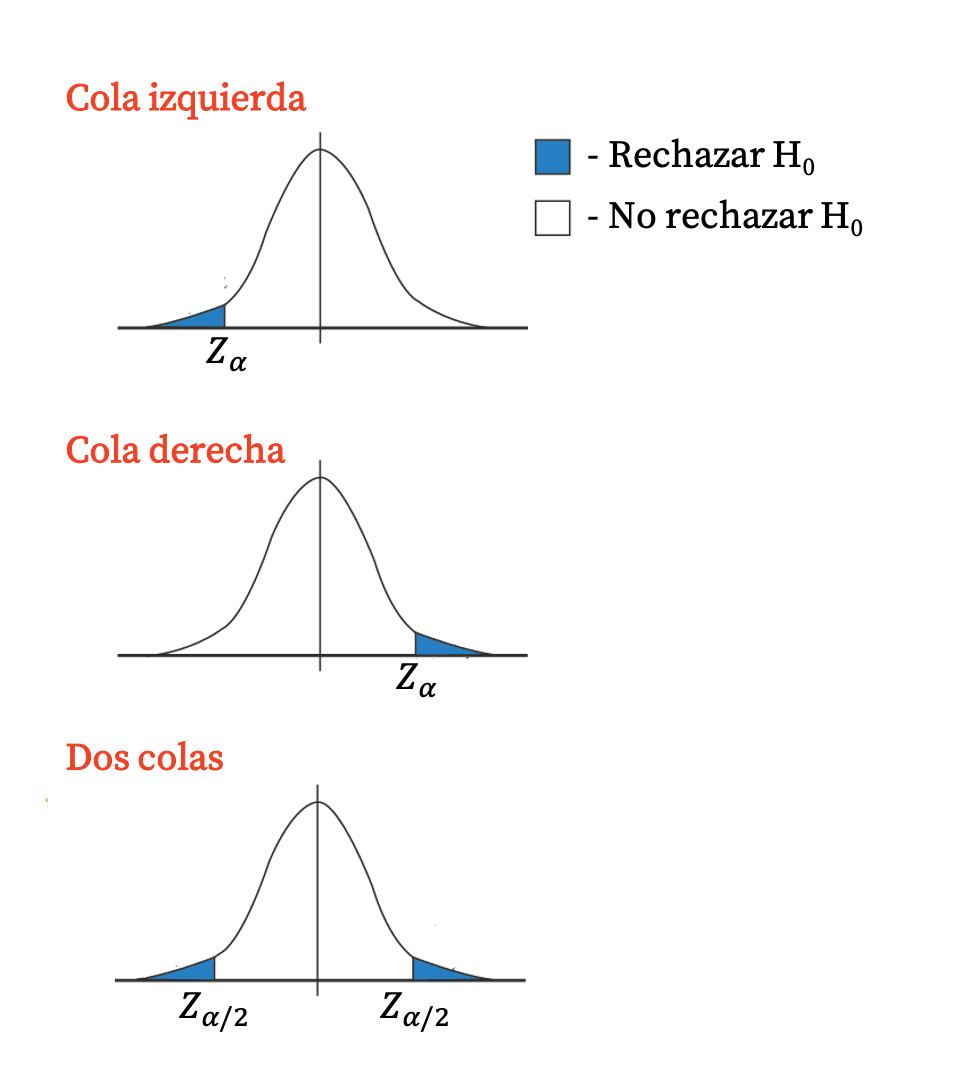
假设检验的临界值
临界值还可用于假设检验,以拒绝原假设(并接受备择假设)或拒绝备择假设(并接受原假设)。
- 如果与 p 值对应的检验统计量的分布值位于临界值标记的区间内,则不拒绝零假设(拒绝备择假设)。
- 如果与 p 值对应的检验统计量的分布值超出临界值标记的区间,则拒绝原假设(接受备择假设)。