为什么标准差很重要？ （解释+示例）

标准差用于衡量样本中数值的分布情况。

我们可以使用以下公式来计算给定样本的标准差：

√ Σ( _xi – x _bar ) ² / (n-1)

金子：

• Σ：表示“和”的符号
• x _i :样本的^{第 i 个}值
• x _bar :样本平均值
• n：样本量

标准差值越高，样本中的值越分散。相反，标准差值越低，值的聚类越紧密。

学生经常问的一个问题是：为什么标准差很重要？

答案：标准差很重要，因为它告诉我们给定数据集中值的分布。

每当我们分析数据集时，我们想要找到以下指标：

• 数据集的中心。衡量“中心”的最常见方法是使用平均值和中位数。
• 数据集中值的分布。衡量传播的最常见方法是使用标准差。

通过知道中心在哪里以及值的分布是什么，我们可以很好地理解任何数据集中值的分布。

以下示例说明了标准差在实践中的重要性。

示例1：薪资分配

假设 A 公司的平均工资为 80,000 美元，标准差为 20,000 美元。由于标准偏差如此之大，如果您在这家公司工作，并不能保证您每年的工资会接近 80,000 美元，因为工资存在如此大的差异。

相反，假设 B 公司的平均工资也是 80,000 美元，但标准差仅为 4,000 美元。由于这个标准差非常小，因此您可以确定您将获得接近 80,000 美元的工资，因为工资变化很小。

如果我们创建一个箱线图来可视化这两家公司的薪资分布，它可能如下所示：

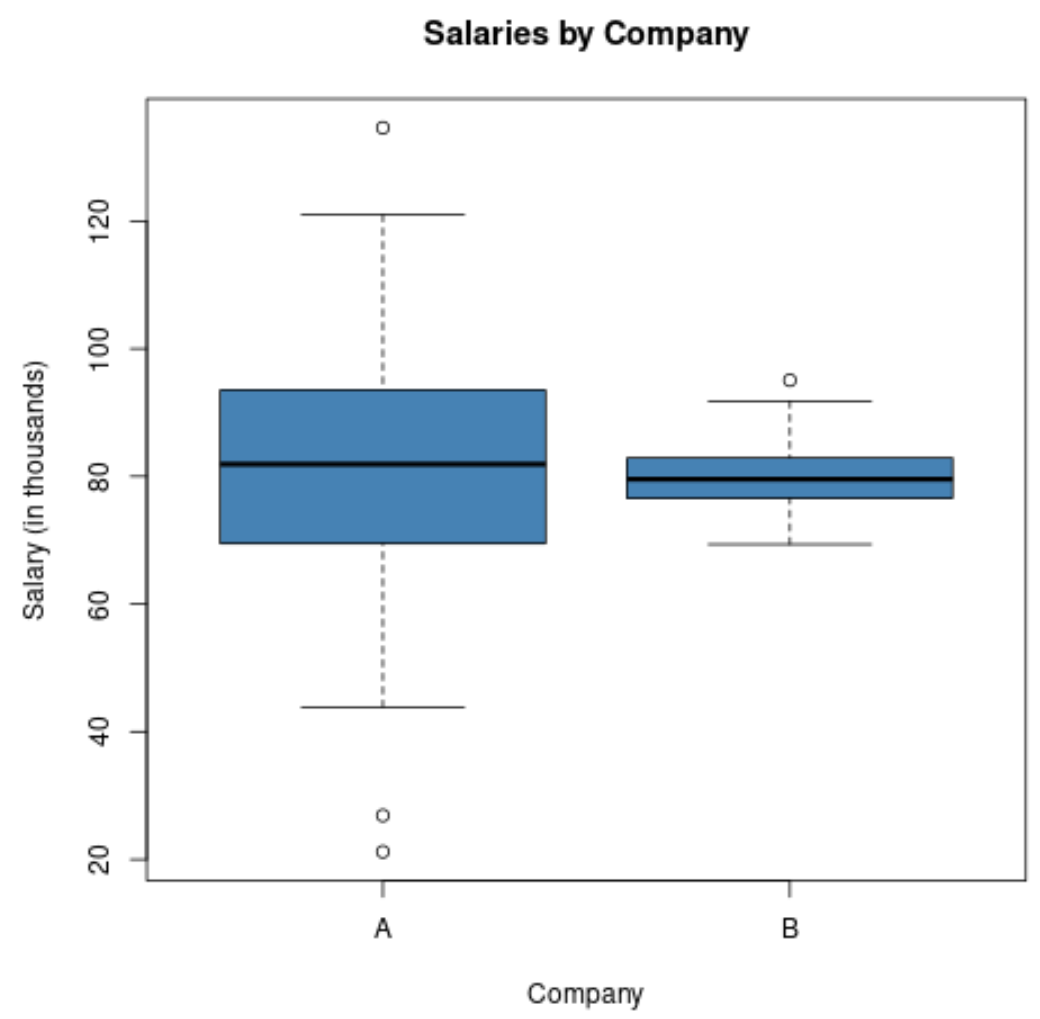
请注意，由于工资的标准差较高，A 公司箱线图的长度也较长。

两家公司的平均工资相同，但A公司的工资差距要大得多。

例2：房价分布

假设 A 社区的平均房价为 250,000 美元，标准差为 50,000 美元。由于标准差相当大，这意味着一些房价将远高于 250,000 美元，而另一些则低得多。如果您查看该社区的任何特定房屋，都不能保证价格会接近平均水平。

相反，假设 B 社区的平均房价也是 250,000 美元，但标准差仅为 10,000 美元。由于这个标准偏差非常小，因此您可以确定您在附近看到的任何房子都可能会以这个价格成交。

如果我们创建一个箱线图来可视化这两个社区的房价分布，它可能如下所示：

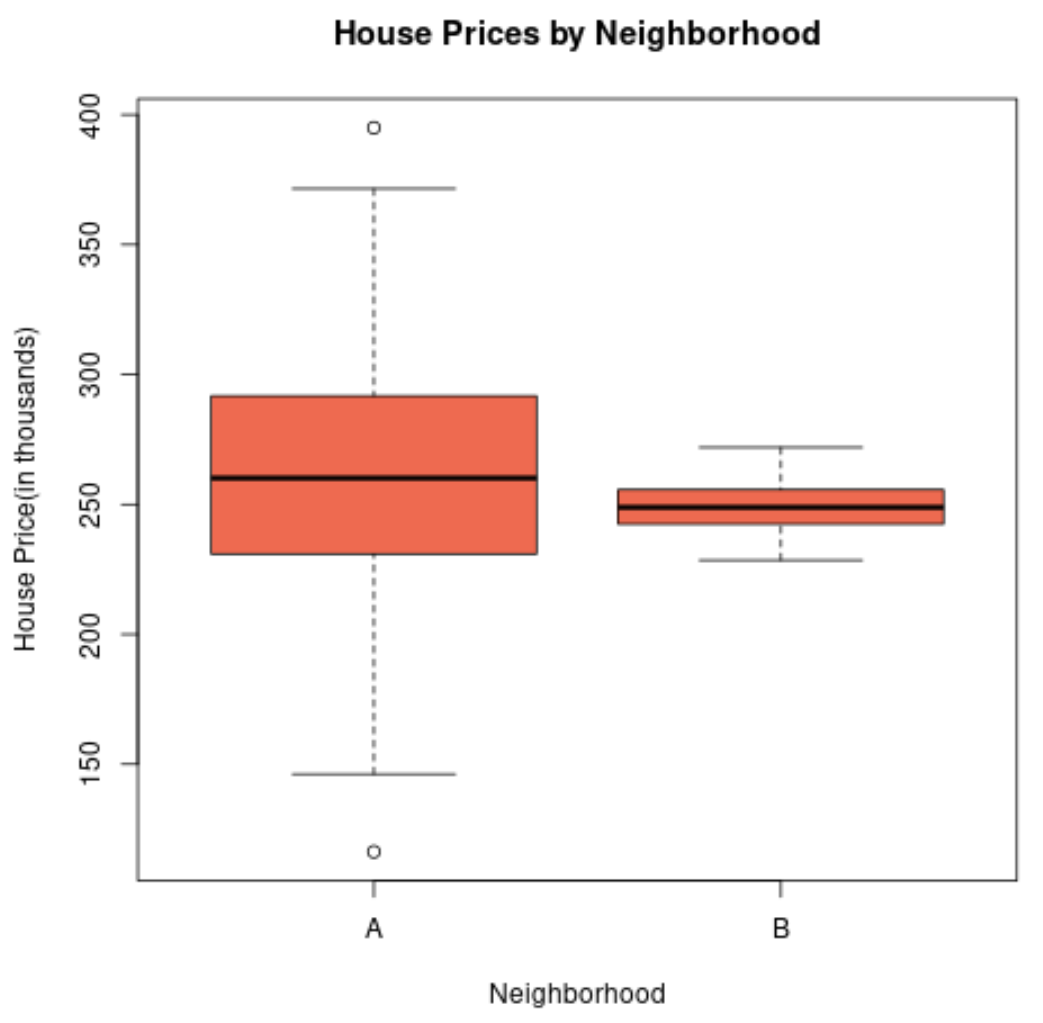
房地产价格的标准差越高，邻域 A 的箱线图的长度就越大。

事实上，A区的房价从不到15万美元到40万美元以上不等，而B区的房价只有23万美元到27万美元左右。

通过简单地了解每个社区房价的标准差，我们就可以知道每个社区的价格预期会有多少变化。

其他资源

什么被认为是好的标准差？
范围对比标准差：何时使用每个标准差
变异系数与标准差：差异