为什么样本量很重要? (解释和示例)
样本量是指参与实验或研究的总人数。
样本大小很重要,因为它直接影响我们估计总体参数的精度。
要理解为什么会出现这种情况,对置信区间有基本的了解会有所帮助。
置信区间的简要解释
在统计学中,我们经常寻求测量总体参数——描述整个总体某些特征的数字。
例如,我们可能有兴趣测量某个城市中所有人的平均身高。
然而,收集群体中每个个体的数据通常过于昂贵且耗时。所以我们通常从总体中随机抽取样本,并使用样本数据来估计总体参数。
例如,我们可以收集城市中 100 名随机个体的身高数据。然后我们可以计算样本中个体的平均大小。然而,我们不能确定样本均值与总体均值完全匹配。
为了解释这种不确定性,我们可以创建一个置信区间。置信区间是可能包含具有一定置信水平的总体参数的值范围。
计算总体平均值置信区间的公式为:
置信区间 = x +/- z*(s/√ n )
金子:
- x :样本平均值
- z:选择的z值
- s:样本标准差
- n:样本量
您使用的 z 值取决于您选择的置信水平。下表显示了与最常见的置信水平选择相对应的 z 值:
| 一定程度的信心 | z值 |
|---|---|
| 0.90 | 1,645 |
| 0.95 | 1.96 |
| 0.99 | 2.58 |
样本量和置信区间之间的关系
假设我们想要估计一群海龟的平均重量。我们随机收集海龟样本,其中包含以下信息:
- 样本量n = 25
- 平均样本重量x = 300
- 样本标准差s = 18.5
以下是计算真实总体平均体重的 90% 置信区间的方法:
90% 置信区间: 300 +/- 1.645*(18.5/√ 25 ) = [293.91, 306.09]
我们 90% 确信海龟种群中的实际平均体重在 293.91 至 306.09 磅之间。
现在假设我们收集 50 只海龟的数据,而不是 25 只海龟。
以下是计算真实总体平均体重的 90% 置信区间的方法:
90% 置信区间: 300 +/- 1.645*(18.5/√ 50 ) = [295.79, 304.30]
请注意,此置信区间比之前的置信区间更窄。这意味着我们对海龟种群真实平均重量的估计更加准确。
现在假设我们收集 100 只海龟的数据。
以下是计算真实总体平均体重的 90% 置信区间的方法:
90% 置信区间: 300 +/- 1.645*(18.5/√ 100 ) = [296.96, 303.04]
请注意,此置信区间甚至比之前的置信区间更窄。
下表总结了每个置信区间宽度:
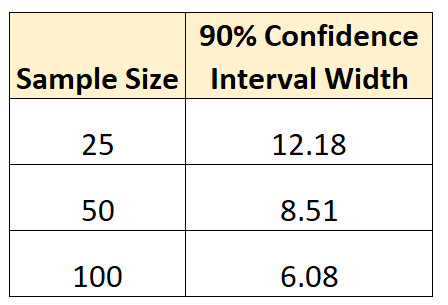
底线是:样本量越大,我们可以更准确地估计总体参数。
其他资源
以下教程提供了有关置信区间和样本大小的更有用的解释。