事件交叉的概率

本文解释了如何计算事件交叉的概率。所以你会发现事件交叉概率的公式是什么，此外还有逐步解决的练习。

事件的交集是什么？

在概率论中，事件的交集是事件的运算，其结果由该运算的所有事件共有的基本事件组成。也就是说，事件A和B的交集是由同时属于A和B的所有事件形成的。

两个事件的交集用符号⋂表示。因此，事件 A 和 B 的交集写作 A⋂B。

例如，在掷骰子的随机实验中，如果一个事件是掷出偶数 A={2, 4, 6}，另一事件是掷出大于 3 的数字 B={4, 5， 6 }，两个事件的交集为 A⋂B={4, 6}。

事件交叉概率的公式

两个事件相交的概率等于一个事件发生的概率乘以给定第一个事件时另一个事件发生的条件概率。

因此，两个事件相交的概率公式为 P(A⋂B)=P(A) P(B|A)=P(B) P(A|B)。

金子：

• 

  和

  

  这是两个相关事件。

• 

  是事件 A 和事件 B 相交的概率。

• 

  是事件 A 发生的概率。

• 

  是给定事件 A 时事件 B 发生的条件概率。

• 

  是事件 B 发生的概率。

• 

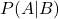
  是给定事件 B 时事件 A 发生的条件概率。

但是，如果两个事件是独立的，则意味着一个事件发生的概率不依赖于另一个事件是否发生。因此，两个独立事件相交的概率公式如下：

金子：

• 

  和

  

  这是两个独立的事件。

• 

  是事件 A 和事件 B 相交的概率。

• 

  是事件 A 发生的概率。

• 

  是事件 B 发生的概率。

事件交叉概率的真实示例

接下来，我们给您留下两个逐步解决的示例，以便您了解如何计算两个事件相交的概率。我们将首先看到两个独立事件的交集示例，然后是两个相关事件的交集示例，因此您可以看到这两种情况。

两个独立事件相交的概率

• 抽签连续进行3次。求三次抛掷都得到正面的概率。

在这种情况下，我们要计算联合概率的事件是独立的，因为抽签的结果不依赖于前一次抽签获得的结果。因此，要确定连续获得三个正面的概率，我们必须使用独立事件的交集概率公式：

抽签的时候，只有两种可能的结果：正面或反面。因此，抛硬币时正面或反面出现的概率为：

因此，为了求出所有 3 次抛硬币都出现正面的概率，我们需要将出现正面的概率乘以 3：

简而言之，连续 3 次正面朝上的概率为 12.5%。

两个相关事件相交的概率

• 在一个空盒子里，我们放入 8 个蓝色球、4 个橙色球和 2 个绿色球。如果我们先抽一个球，然后再抽另一个球，而不将第一个抽出的球放回盒子里，那么第一个球是蓝色的，第二个球是橙色的概率是多少？

在这种情况下，事件是相关的，因为在第二次抽奖中拿起橙色球的概率取决于在第一次抽奖中抽出的球的颜色。因此，为了计算问题要求我们的概率，我们必须使用相关事件的交叉概率公式：

第一次抽奖中获得蓝球的概率很容易确定，只需将蓝球的数量除以球的总数即可：

另一方面，在拿走蓝色球后抽出橙色球的概率的计算方式有所不同，因为橙色球的数量不同，此外，现在盒子内少了一个球：

因此，首先绘制蓝色球然后绘制橙色球的概率是通过将上面找到的两个概率相乘来计算的：

事件相交属性

在概率论中，事件的交集具有以下属性：

• 交换性：交集事件的顺序不改变运算结果。

• 关联性：三个事件的交集可以按任何顺序计算，因为结果是相同的。

• 分配律：事件的交集满足事件并集处的分配律。