什么是二分变量？ （定义&#038；示例）

二分变量是一种仅采用两个可能值的变量类型。

以下是二分变量的一些示例：

• 性别：男或女
• 抛硬币：正面还是反面
• 房产类型：住宅或商业
• 运动员身份：职业或业余
• 考试结果：通过或失败

这些类型的变量在实践中时常出现。例如，考虑以下包含 10 个观测值和 4 个变量的数据集：

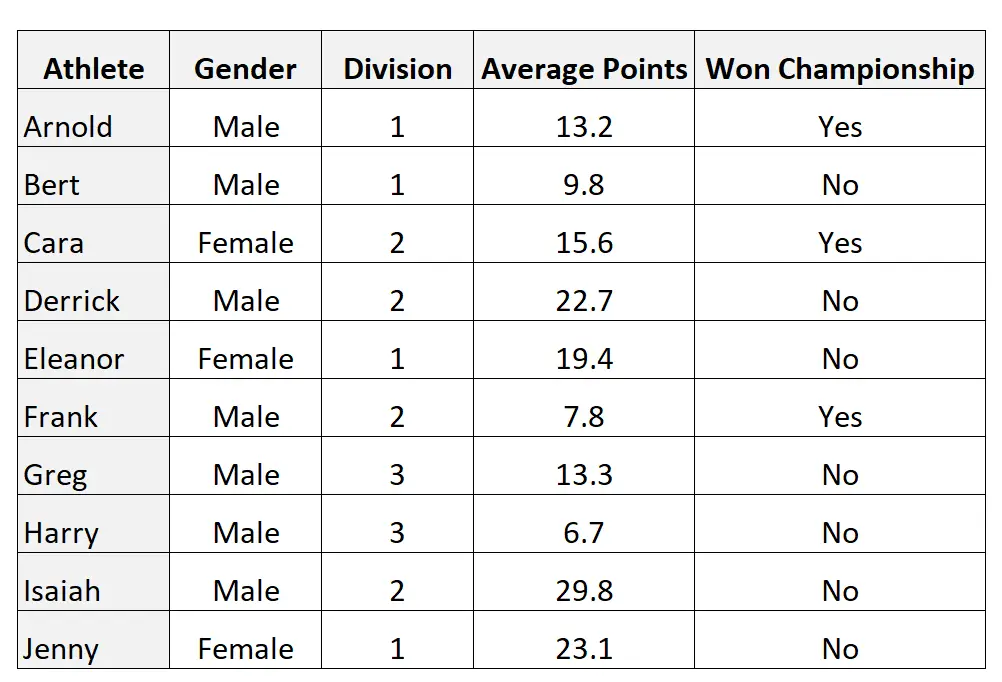
变量性别和赢得的冠军是二分的，因为它们只能采用两个可能的值：

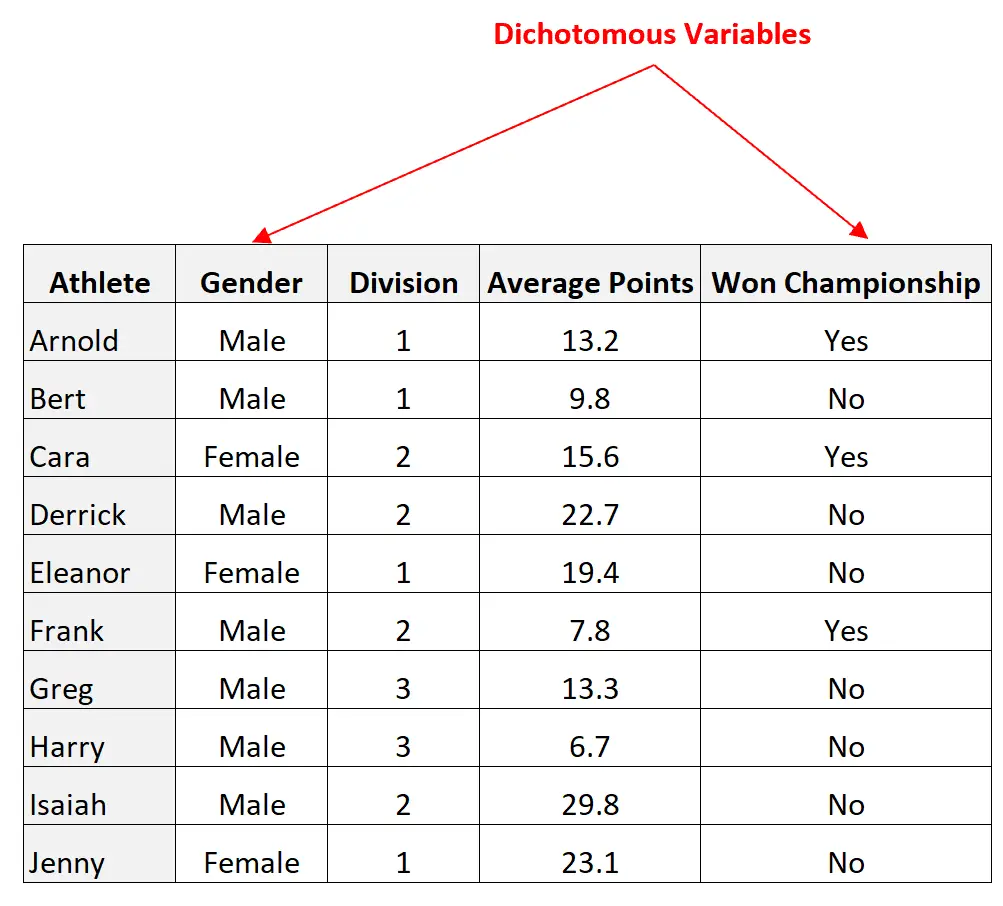
但是，除法和平均点变量不是二分法，因为它们可以采用多个值。

额外提示：

您可以通过记住前缀“di”是希腊单词，意思是“两个”、“两次”或“双倍”来记住二分变量只能取两个值。

如何创建二分变量

需要注意的是，我们可以通过简单地根据某个阈值分离值来从连续变量创建二分变量。

例如，在前面的数据集中，我们可以将平均得分变量转换为二分变量，将平均得分高于 15 的球员分类为“好得分手”，将平均得分低于 15 的球员分类为“糟糕得分手”：

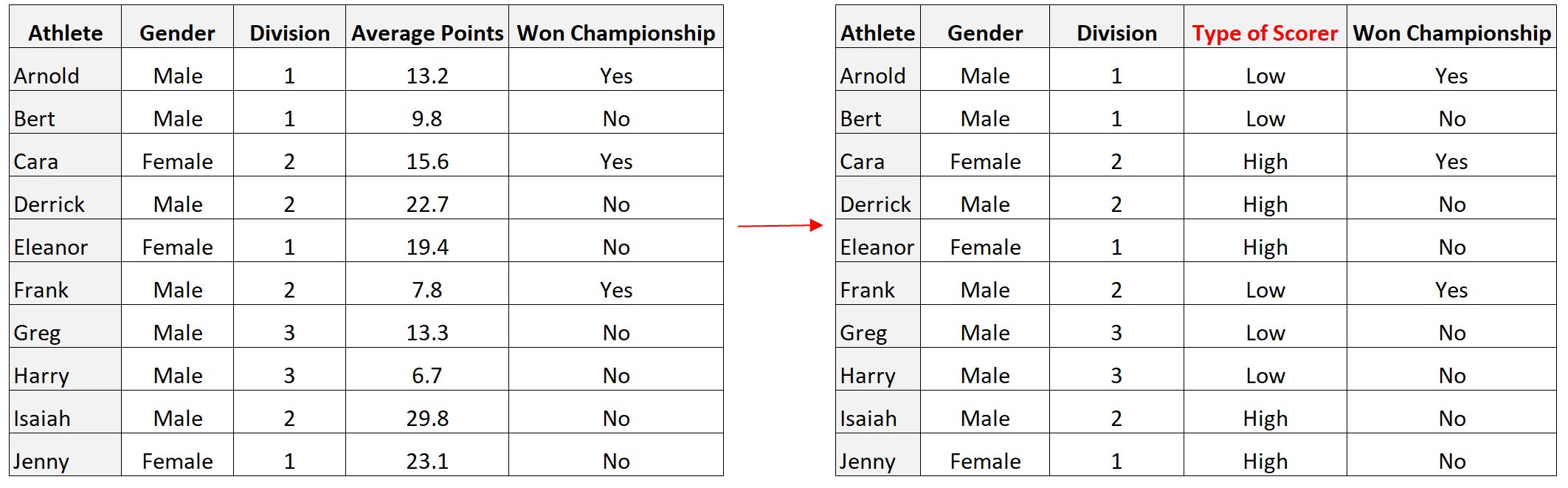
如何可视化二分变量

我们通常使用简单的条形图来可视化二分变量，以表示它们可以采用的每个值的频率。

例如，以下条形图显示了先前数据集中每种性别的频率：

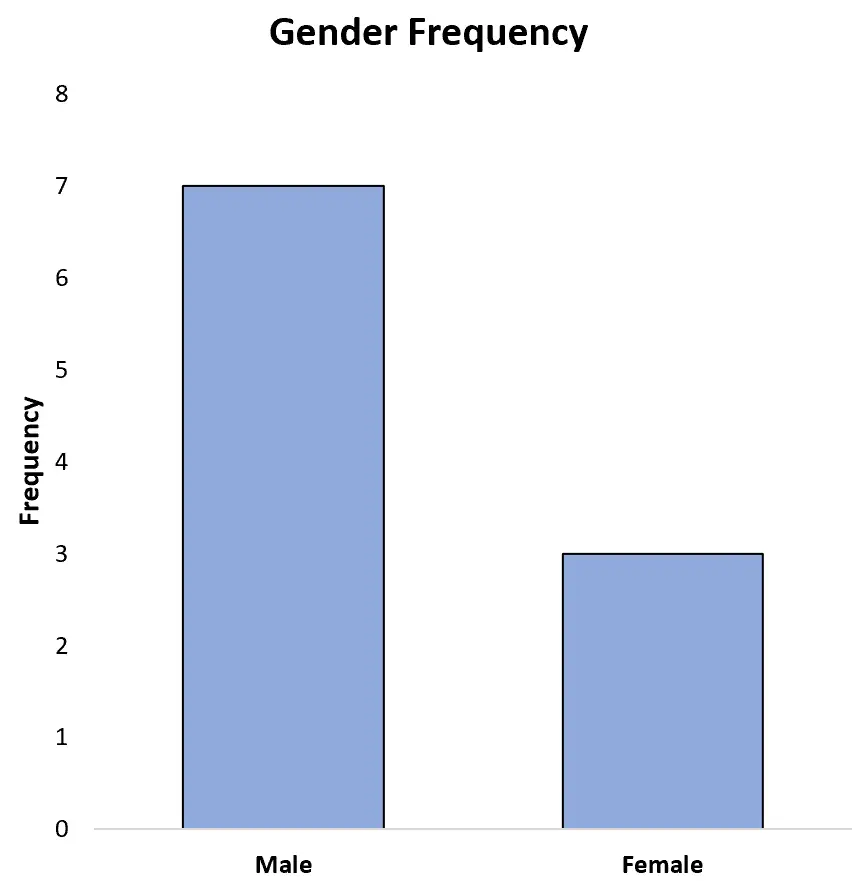
我们还可以在 y 轴上将频率显示为百分比：

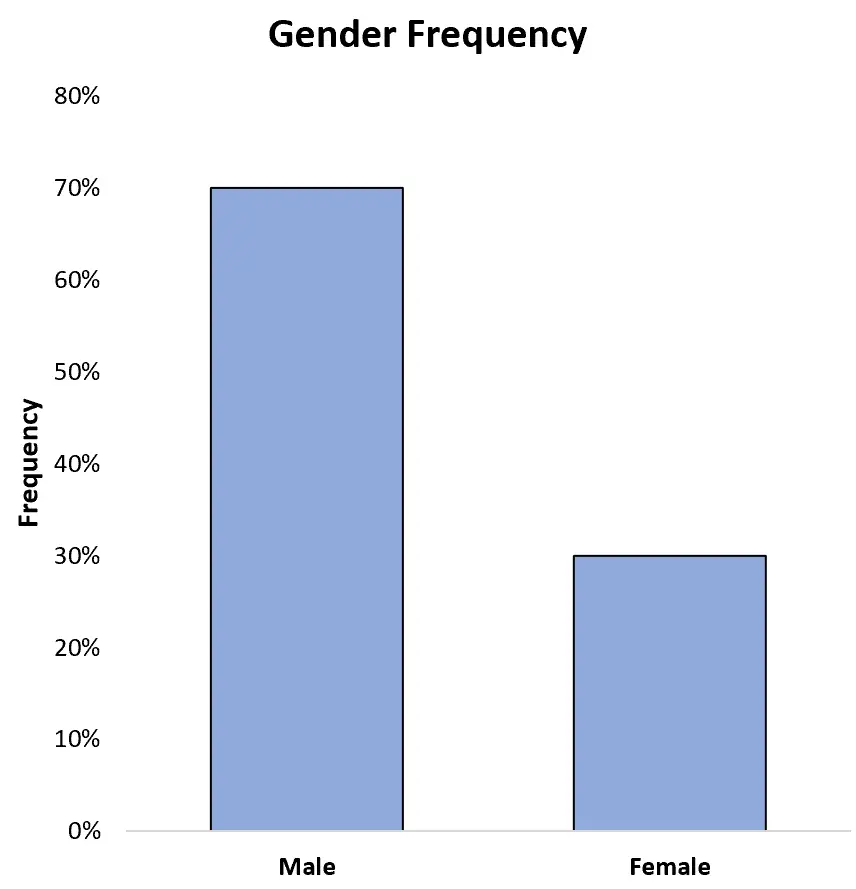
这让我们很容易看到数据集中运动员总数的 70% 是男性，30% 是女性。

如何分析二分变量

有多种方法可以分析二分变量。两种最常见的方法包括：

1.单比例z检验

一比例 z 检验确定观察到的比例是否等于理论比例。

例如，我们可以使用此测试来确定给定人群中男性运动员的真实比例是否等于 50%。

2. 点双列相关

点二列相关用于衡量二分变量和连续变量之间的关系。

这种类型的相关性取 -1 到 1 之间的值，其中：

• -1表示两个变量之间完全负相关
• 0 表示两个变量之间没有相关性
• 1 表示两个变量之间完全正相关

例如，我们可以计算性别和每场比赛平均得分之间的双列相关性，以了解这两个变量的相关程度。