二项分布

经过本杰明·安德森博 8月 3, 2023 可能性 0 条评论

本文解释了统计学中的二项分布是什么以及它的用途。因此，您将找到二项式分布的定义、二项式分布的示例以及此类概率分布的属性。此外，您将能够使用在线计算器计算二项式分布的任何概率。

什么是二项分布？

二项式分布是一种概率分布，用于计算以恒定的成功概率执行一系列独立的二分实验时的成功次数。

换句话说，二项分布是描述一系列伯努利试验的成功结果数量的分布。

请记住，伯努利测试是一种有两种可能结果的实验：“成功”和“失败”。因此，如果“成功”的概率为p ，则“失败”的概率为q=1-p 。

一般来说，执行的实验总数由参数n定义，而p是每个实验成功的概率。因此，服从二项式分布的随机变量可写为：

$X\sim\text{Bin}(n,p)$

请注意，在二项分布中，完全相同的实验重复n次，并且实验彼此独立，因此每次实验成功的概率是相同的(p) 。

二项分布也可称为二项分布。

二项式分布示例

一旦我们了解了二项式分布的定义，我们将看到遵循这种类型分布的变量的几个示例，以更好地理解这个概念。

抛硬币 25 次，正面出现的次数。
篮球运动员从同一位置向篮筐投篮 60 次时的出手次数。
掷骰子 30 次得到数字 6 的次数。
总共 50 名参加考试的学生中通过的人数。
100 个产品样本中的缺陷单元数。

二项分布公式

给定参数x、n、p，二项式分布的概率函数定义为x中的n乘以p ^x乘以(1-p) ^nx的组合数。

因此，二项分布概率的计算公式为：

二项分布公式

👉您可以使用下面的计算器来计算变量服从二项式分布的概率。

另一方面，二项式分布的累积概率是通过将相关成功案例数量的概率与所有先前概率相加来计算的。因此，计算二项式分布累积概率的公式为：

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

解决了二项式分布的练习

我们抛硬币 10 次，得到 6 次正面的概率是多少？

该问题中的变量服从二项式分布，因为所有发射都是相互独立的，并且也具有相同的成功概率。

具体来说，成功的概率是 50%，因为两种可能结果中只有一种被认为是成功的。

$p=\cfrac{1}{2}=0,5$

因此，本次练习的分布是二项式，共有 10 次实验，概率为 0.5。

$X\sim\text{Bin}(10 ; 0,5)$

因此，为了确定获得六个正面的概率，我们需要应用二项式分布公式。

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

因此，抛硬币 10 次，恰好得到 6 个正面的概率是 20.51%。

二项分布的特征

二项式分布具有以下特点：

二项式分布由两个参数定义： n是伯努利实验的总数， p是每个伯努利实验成功的概率。

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

二项式分布的平均值等于实验总数乘以每个实验成功概率的乘积。因此，要计算二项分布的平均值，必须将n乘以p 。

$E[X]=n\cdot p$

二项式分布的方差等于试验总数乘以成功概率和失败概率。

$Var(X)=n\cdot p\cdot (1-p)$

二项式分布的概率函数公式如下：

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

类似地，二项式分布的累积分布函数的公式为：

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

具有相同概率的两个独立二项式分布之和相当于具有相同概率值p和n的二项式分布，即两个分布的试验总数之和。

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

伯努利分布是二项式分布的一种特殊情况，其中n=1 ，即仅进行一次实验。

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_如果_X 1 , _X ₂ ,…, X _k是独立的随机变量，使得

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

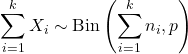
二项式分布计算器

将二项式分布的参数p、n和x的值输入到下面的计算器中，计算概率。您需要选择要计算的概率，并使用点作为小数分隔符输入数字，例如 0.1667。

关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多

添加评论