机器学习中的偏差-方差权衡是什么?
为了评估模型在数据集上的性能,我们需要测量模型的预测与观察到的数据的匹配程度。
对于回归模型,最常用的指标是均方误差(MSE),其计算如下:
MSE = (1/n)*Σ(y i – f(x i )) 2
金子:
- n:观察总数
- y i :第 i 个观测值的响应值
- f( xi ):第 i个观测值的预测响应值
模型预测与观测值越接近,MSE 就越低。
然而,我们只关心MSE 测试——当我们的模型应用于看不见的数据时的 MSE。这是因为我们只关心模型在未知数据上的表现,而不是在现有数据上的表现。
例如,如果预测股票价格的模型在历史数据上的 MSE 较低,那也没关系,但我们确实希望能够使用该模型来准确预测未来数据。
事实证明,MSE测试仍然可以分为两部分:
(1) 方差:指的是如果我们使用不同的训练集来估计函数f 的变化量。
(2)偏差:指用简单得多的模型来处理可能极其复杂的实际问题而引入的误差。
用数学术语写成:
MSE 检验 = Var( f̂( x 0 )) + [偏差( f̂( x 0 ))] 2 + Var(ε)
MSE 检验 = 方差 + 偏差2 + 不可约误差
第三项是不可约误差,是任何模型都无法约简的误差,因为解释变量集与响应变量之间的关系中始终存在噪声。
具有高偏差的模型往往具有低方差。例如,线性回归模型往往具有高偏差(假设解释变量和响应变量之间存在简单的线性关系)和低方差(模型估计值在样本之间不会有太大变化)。另一个)。
然而,低偏差的模型往往具有高方差。例如,复杂的非线性模型往往具有低偏差(不假设解释变量和响应变量之间存在某种关系)和高方差(模型估计值从一个学习样本到另一个学习样本可能会发生显着变化)。
偏差与方差的权衡
偏差-方差权衡是指当我们选择减少偏差(通常会增加偏差)或减少方差(通常会增加偏差)时发生的权衡。
下图提供了一种可视化这种权衡的方法:
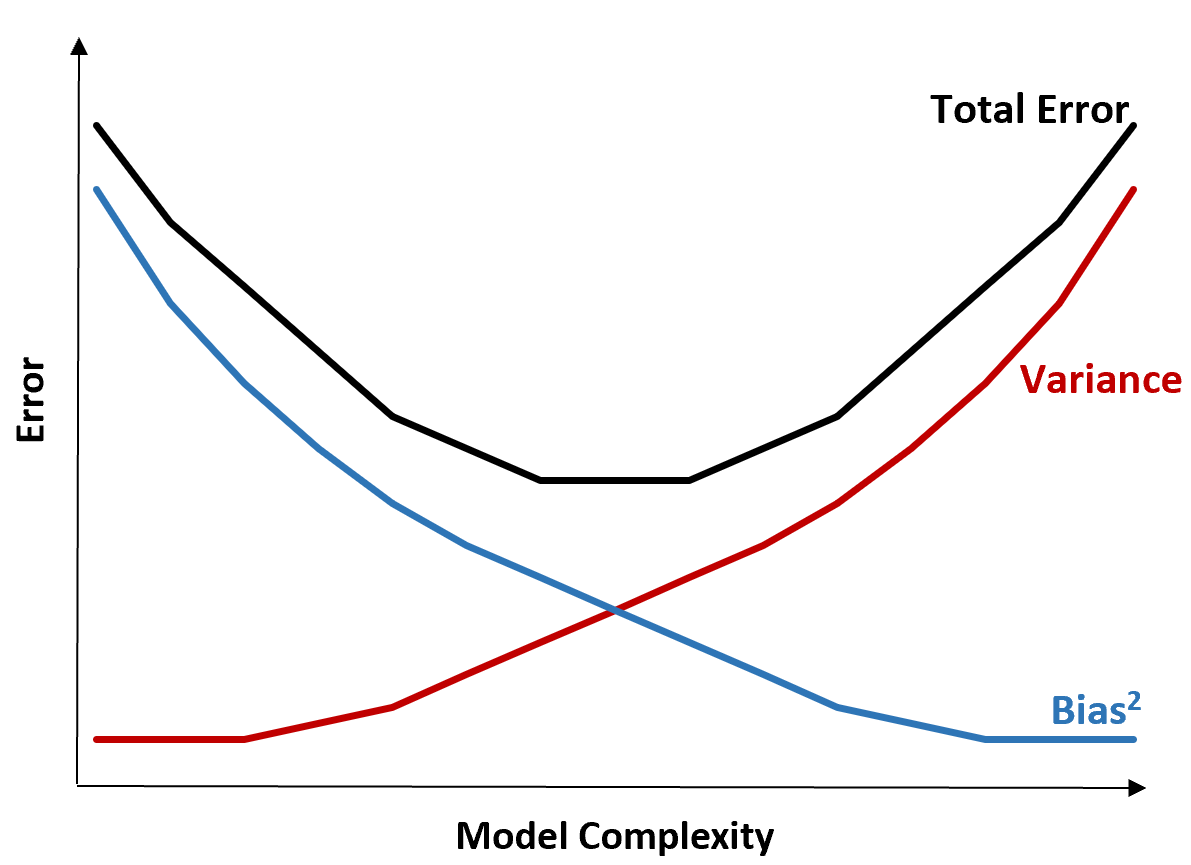
总误差随着模型复杂性的增加而减少,但仅限于某一点。超过某个点后,方差开始增加,总误差也开始增加。
在实践中,我们只关心最小化模型的总误差,而不一定最小化方差或偏差。事实证明,最小化总误差的方法是在方差和偏差之间找到适当的平衡。
换句话说,我们想要一个足够复杂的模型来捕获解释变量和响应变量之间的真实关系,但又不会太复杂而无法检测实际不存在的模式。
当模型过于复杂时,就会过度拟合数据。发生这种情况是因为很难在训练数据中找到纯粹由偶然引起的模式。这种类型的模型可能在不可见数据上表现不佳。
但当模型太简单时,它就会低估数据。发生这种情况是因为假设解释变量和响应变量之间的真实关系比实际情况更简单。
在机器学习中选择最佳模型的方法是在偏差和方差之间找到平衡,以最小化在未来未见过的数据上测试模型的误差。
在实践中,最小化测试 MSE 的最常见方法是使用交叉验证。