如何在 stata 中执行 kruskal-wallis 检验
Kruskal-Wallis 检验用于确定三个或更多独立组的中位数之间是否存在统计显着差异。它被认为是单向方差分析的非参数等效项。
本教程介绍如何在 Stata 中执行 Kruskal-Wallis 检验。
如何在 Stata 中执行 Kruskal-Wallis 检验
对于此示例,我们将使用人口普查数据集,其中包含美国所有 50 个州的 1980 年人口普查数据。在数据集中,各州分为四个不同的区域:
- 北部
- 中北部
- 南
- 西方
我们将进行 Kruskal-Wallis 检验,以确定这四个地区的中位年龄是否相等。
步骤1:加载并显示数据。
首先,通过在命令框中键入以下命令来加载数据集:
使用https://www.stata-press.com/data/r13/census
使用以下命令获取数据集的快速摘要:
总结一下
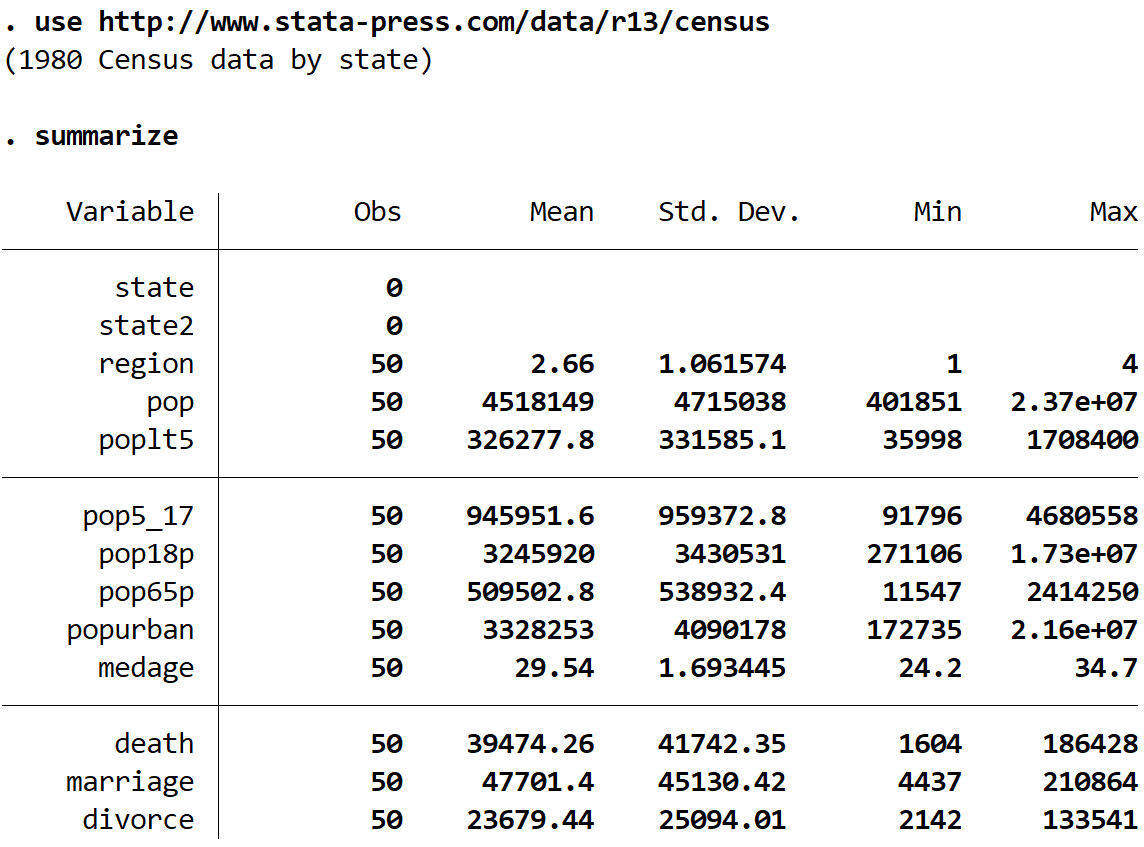
我们可以看到该数据集中有 13 个不同的变量,但我们将使用的唯一两个变量是medage (中位年龄)和Region 。
第 2 步:可视化数据。
在执行 Kruskal-Wallis 检验之前,我们首先创建一些箱线图来可视化四个区域中每个区域的中位年龄分布:
中号图形框,位于(区域)
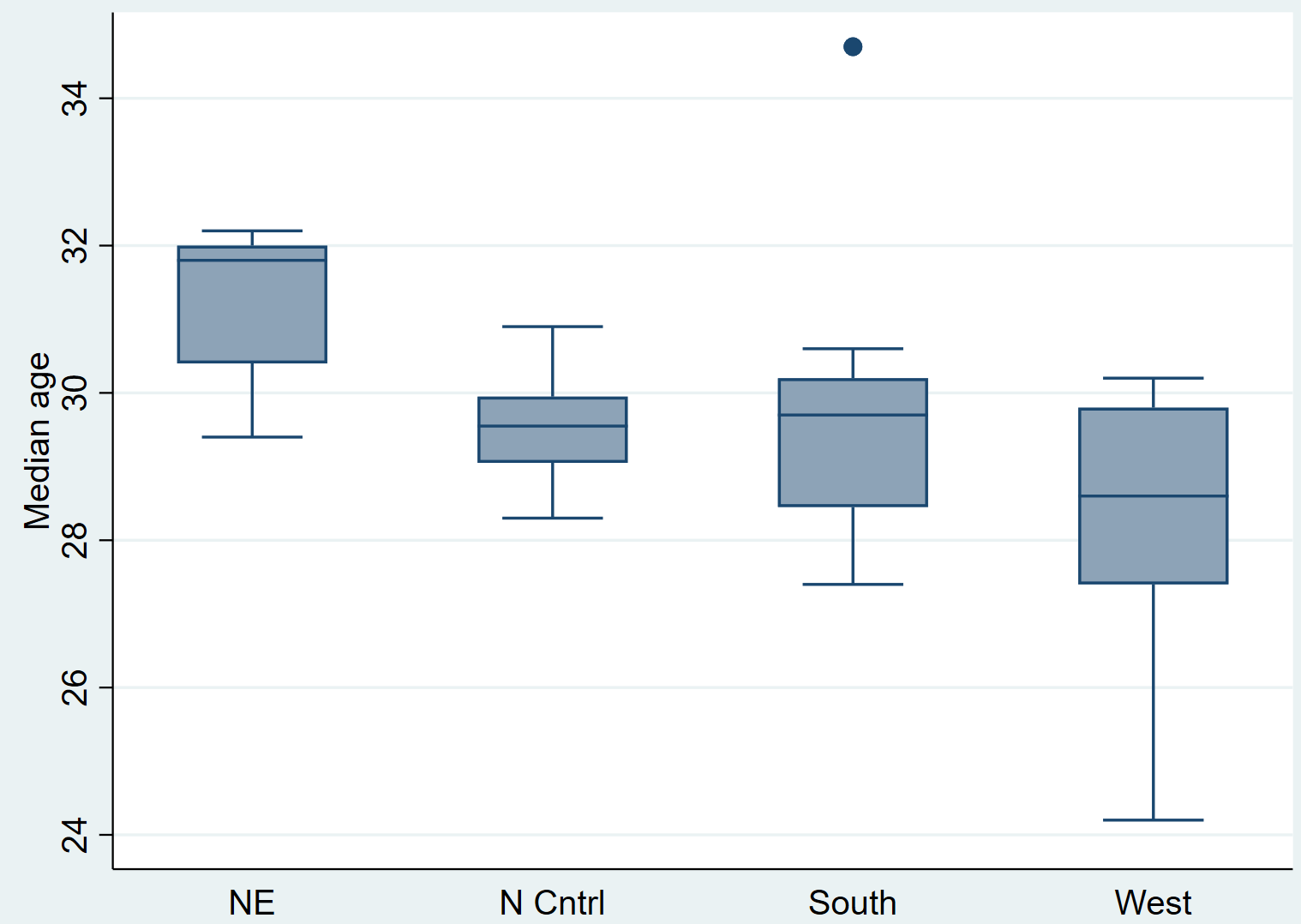
只需查看箱线图,您就可以看到分布似乎因地区而异。然后,我们将执行 Kruskal-Wallis 检验,看看这些差异是否具有统计显着性。
步骤 3:执行 Kruskal-Wallis 检验。
使用以下语法执行 Kruskal-Wallis 测试:
kwallis 测量变量,通过 (grouping_variable)
在我们的例子中,我们将使用以下语法:
kwallis medage,作者(地区)
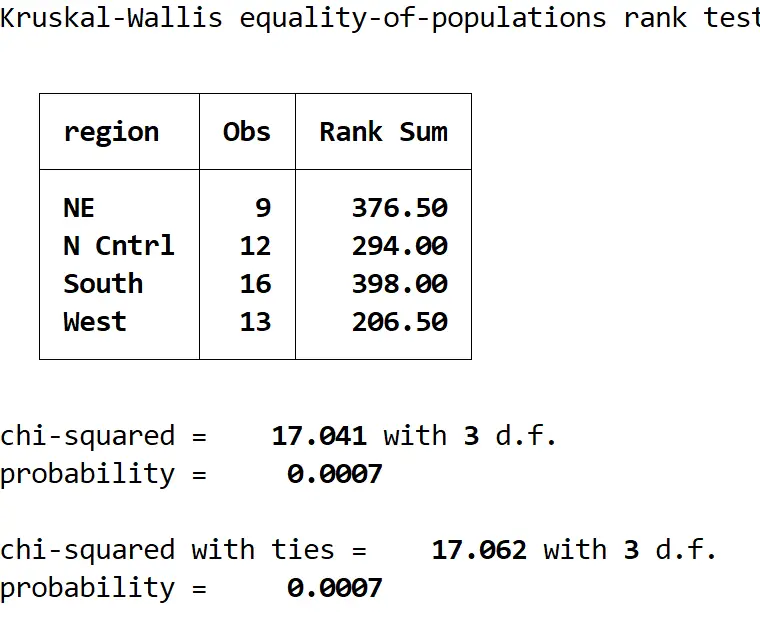
以下是如何解释结果:
汇总表:此表显示每个区域的观察数量以及每个区域的排名总和。
带关系的卡方:这是检验统计量的值,结果为 17.062。
概率:这是对应于检验统计量的 p 值,结果为 0.0007。由于该值小于 0.05,因此我们可以拒绝原假设并得出结论:四个区域的中位年龄不相等。
第四步:报告结果。
最后,我们想报告 Kruskal-Wallis 测试的结果。以下是如何执行此操作的示例:
进行 Kruskal-Wallist 检验以确定美国以下四个地区的个体中位年龄是否相同:
- 东北 (n=9)
- 中北部 (n=12)
- 南 (n=16)
- 西 (n=13)
测试显示,四个地区个体的中位年龄并不相同(X 2 = 17.062,p = 0.0007)。也就是说,两个或多个地区之间的中位年龄存在统计学上的显着差异。