加法规则（或加法规则）

本文解释什么是加法规则，也称为加法规则，以及它在概率和统计中的用途。此外，您将能够看到加法规则的公式是什么，并解决了展示如何使用它的练习。

什么是加法规则（或加法规则）？

加法规则（或加法规则）指出，两个事件的概率之和等于每个事件单独发生的概率之和减去两个事件同时发生的概率。

因此，加法规则的公式为P(A⋃B)=P(A)+P(B)−P(A⋂B)。

因此，要添加两个概率，我们不能简单地添加每个概率，因为我们还必须减去表示两个事件的联合概率的项。然而，在某些情况下，只有将每个事件的概率相加，才能得到概率总和的正确结果。下面我们就来看看这些案例都有哪些。

简而言之，加法规则用于计算一个事件或另一个事件发生的概率，即两个可能事件中至少一个发生的概率。

加法规则公式

加法规则表示，要计算事件 A 或事件 B 发生的概率，我们必须将事件 A 发生的概率加上事件 B 发生的概率，并减去两个事件同时发生的概率。 。

因此，加法规则（或加法规则）的公式如下：

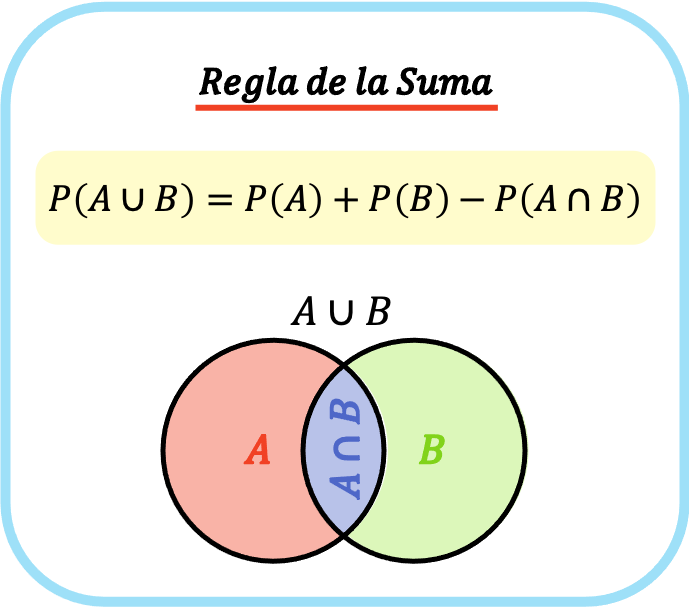
金子：

• 

  是事件A或事件B的概率。

• 

  是事件 A 发生的概率。

• 

  是事件 B 发生的概率。

• 

  是事件A和事件B发生的联合概率。

因此，要使用求和规则，您需要知道如何计算两个事件的联合概率。您可以在以下链接中查看这是如何完成的：

独占事件的求和规则示例

为了完全理解这个概念，让我们看一个如何应用加法规则的示例。

• 我们将 10 个蓝色球、6 个橙色球和 4 个绿色球放入一个盒子中。抽到蓝色或橙色球的概率是多少？

该练习要求我们确定一个或另一个事件发生的概率。因此，解决该问题需要用到加法规则公式：

因此，我们首先使用拉普拉斯规则计算每个事件单独发生的概率：

然而，在这种情况下，两个事件不能同时发生，因为它们是两个互斥的事件。因此，如果我们画一个蓝色的球，我们就不能再画一个橙色的球，反之亦然。

因此，两个事件的联合概率为零，因此求和规则公式得到简化：

所以抓到蓝球或橙球的概率计算如下：

简而言之，从盒子里抽出蓝色或橙色球的概率是 80%。

非独占事件的附加规则示例

看过事件排他性时加法规则的具体示例后，我们现在将了解事件非排他性时如何使用该法则。

• 如果我们抛硬币两次，至少抛一次硬币正面朝上的概率是多少？

在这种情况下，事件并不相互排斥，因为我们可以在第一次抛出时得到“正面”，在第二次抛出时得到“反面”。因此，加法规则的公式没有简化，如下：

因此，我们首先需要应用拉普拉斯法则来计算抛硬币时出现“正面”的概率：

另外，两个事件是独立的，因此我们可以使用乘积规则计算两个事件的联合概率：

最后，要求两次抛掷中至少一次正面朝下的概率，只需将这些值代入加法规则公式并进行计算：

总之，抛硬币两次，至少出现一次正面的概率为 75%。