半四分位距

本文解释了统计学中的半四分位数范围。因此，您将了解如何计算半四分位距、已解决的练习，以及用于计算任何数据样本的半四分位距的在线计算器。

什么是半四分位距？

半四分位距（或半四分位距）是第一四分位数和第三四分位数之差的一半。因此，要计算半四分位数范围，必须减去第三个四分位数减去第一个四分位数，然后除以二。

半四分位距是衡量分散度的指标，表明中心值的变异性。因此，数据集的半四分位数范围越大，中心的值相对于彼此越分散。

半四分位距的特征之一是它是一个稳健的统计参数，因此异常值不会影响半四分位距。

因此，半四分位间距是类似于统计间隔的离散度度量，因为它通过减去两个四分位数值来指示数据集的变异性。然而，统计范围的计算方式略有不同。

半四分位距公式

半四分位数范围等于第三个四分位数和第一个四分位数之间的差除以二。因此，要计算半四分位数范围，必须先找到第一和第三四分位数，然后将它们相减，最后将相减结果除以二。

因此，半四分位距的计算公式为：

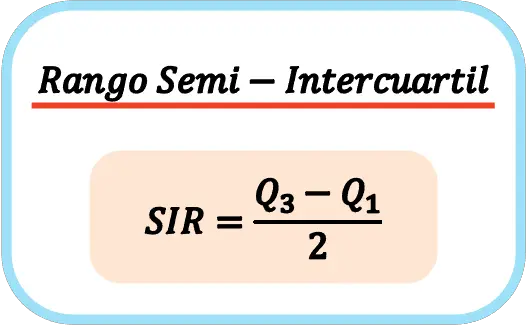
👉您可以使用下面的计算器来计算任何数据集的半四分位数范围。

通常，为了表示半四分位距，通常使用缩写 SIR（半四分位距）作为这种统计度量的符号。

简而言之，半四分位距就是四分位距的一半。

计算半四分位数范围的示例

看完半四分位距的定义及其公式后，下面通过一个具体的例子来清楚地说明半四分位距是如何计算的。

• 我们想要统计分析投资一家公司是否是个好主意。为此，我们收集了该公司过去 15 个月的股价数据。在下表中，您可以看到观察到的数据从最低到最高排序。计算该数据集的半四分位距。

如上一节所述，要找到半四分位数范围，我们必须首先确定第一和第三四分位数。

第一个四分位数是前半部分值的中位数，对应于 8.95 欧元/股的值。

另一方面，第三个四分位数是后半部分值的中间值，即 9.83 欧元/股。

一旦我们知道了第一和第三四分位数的值，我们只需应用半四分位间距的公式即可找到其值：

半四分位距计算器

在以下在线计算器中输入统计数据集以计算其半四分位数范围。数据必须用空格分隔，并使用句点作为小数点分隔符输入。