单向方差分析:定义、公式和示例
单向方差分析(“方差分析”)比较三个或更多独立组的均值,以确定相应总体的均值之间是否存在统计显着差异。
本教程解释了以下内容:
- 执行单向方差分析的动机。
- 执行单向方差分析必须满足的假设。
- 执行单向方差分析的过程。
- 如何执行单向方差分析的示例。
单向方差分析:动机
假设我们想知道三种不同的考试准备课程是否会导致高考平均分数不同。由于全国有数百万高中生,因此向每个学生走遍并让他们使用其中一个备考课程既耗时又昂贵。
相反,我们可以从总体中随机选择100 名学生中的三个样本,并允许每个样本使用三个考试准备程序之一来准备考试。然后我们可以记录每个学生参加考试后的成绩。
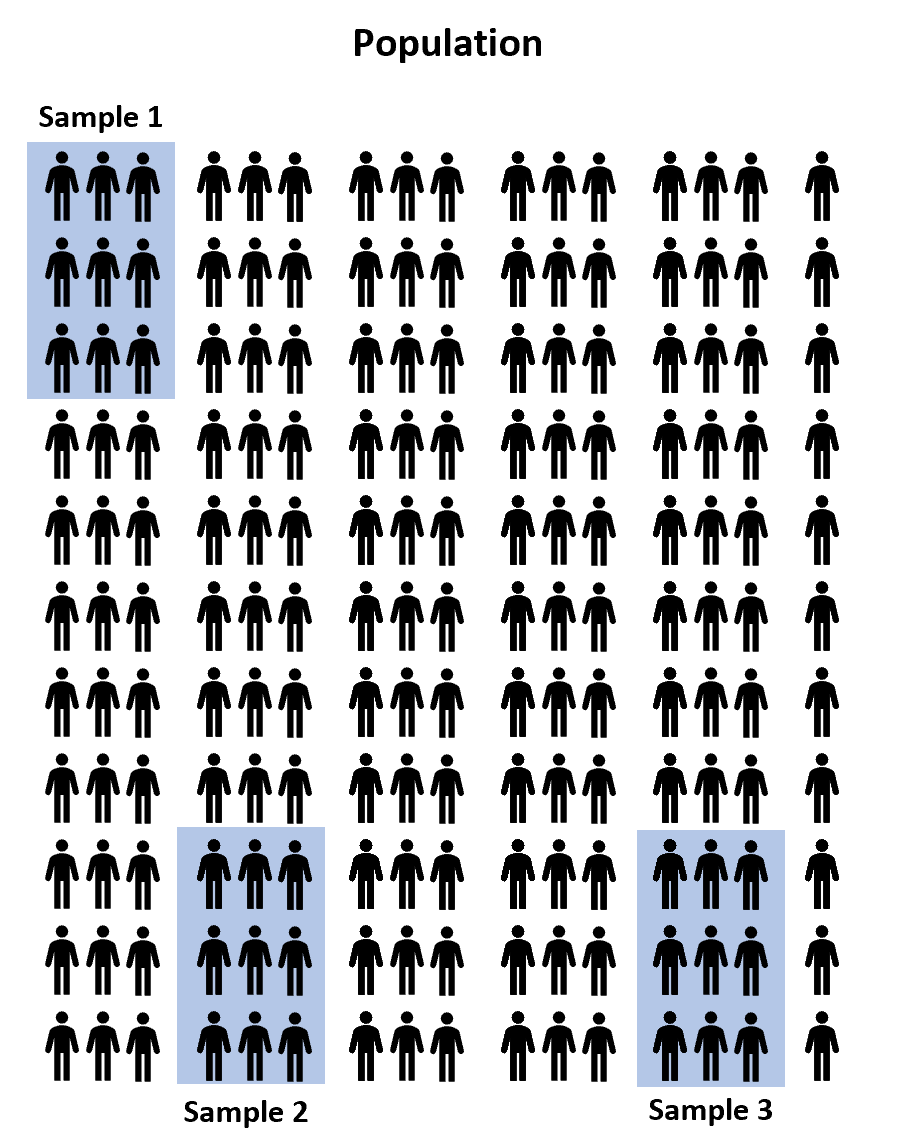
然而,几乎可以保证三个样本之间的平均考试成绩至少会略有不同。问题是这种差异是否具有统计显着性。幸运的是,单向方差分析可以让我们回答这个问题。
单向方差分析:假设
为了使单向方差分析的结果有效,必须满足以下假设:
1. 正态性——每个样本都是从正态分布的总体中抽取的。
2. 方差相等——抽取样本的总体方差相等。您可以使用Bartlett 检验来检验该假设。
3. 独立性——各组内的观察结果彼此独立,并且组内的观察结果是通过随机抽样获得的。
阅读本文以了解有关如何验证这些假设的更多详细信息。
单向方差分析:过程
单向方差分析使用以下原假设和备择假设:
- H 0 (零假设): μ 1 = μ 2 = μ 3 = … = μ k (所有总体平均值相等)
- H 1 (替代假设):至少有一个总体平均值不同 休息
您通常会使用一些统计软件(例如 R、Excel、Stata、SPSS 等)来执行单向方差分析,因为手动执行比较繁琐。
无论您使用什么软件,您都会收到下表作为输出:
| 来源 | 平方和 (SS) | df | 均方 (MS) | F | p |
|---|---|---|---|---|---|
| 治疗 | RSS | df r | MSR | MSR/MSE | df r , df e |
| 错误 | ESS | df | 均方误差 | ||
| 全部的 | 职业健康与安全 | dft |
金子:
- SSR:平方和回归
- SSE:误差平方和
- SST:总平方和(SST = SSR + SSE)
- df r :回归自由度 (df r = k-1)
- df e :误差自由度 (df e = nk)
- df t :总自由度 (df t = n-1)
- k:组总数
- n:观察总数
- MSR:均方回归(MSR = SSR/df r )
- MSE:均方误差(MSE = SSE/df e )
- F: F 检验统计量(F = MSR/MSE)
- p:对应于F dfr, dfe的p值
如果 p 值小于所选的显着性水平(例如 0.05),则您可以拒绝原假设并得出结论:总体均值中至少有一个与其他均值不同。
注意:如果您拒绝原假设,则表明至少有一个总体均值与其他总体均值不同,但 ANOVA 表并未指定哪些总体均值不同。要确定这一点,您需要执行事后测试,也称为“多重比较”测试。
单向方差分析:示例
假设我们想知道三种不同的考试准备计划是否会导致给定考试的平均分数不同。为了测试这一点,我们招募了 30 名学生参加一项研究,并将他们分为三组。
每组的学生被随机分配在接下来的三周内使用三个考试准备计划之一来准备考试。三周结束时,所有学生都参加相同的考试。
各组考试成绩如下:

为了对此数据执行单向方差分析,我们将使用带有以下输入的统计单向方差分析计算器:

从输出表中,我们看到 F 检验统计量为2.358 ,相应的 p 值为0.11385 。

由于该 p 值不小于 0.05,因此我们无法拒绝原假设。
这意味着我们没有足够的证据表明三组的平均考试成绩之间存在统计上的显着差异。
其他资源
以下文章解释了如何使用不同的统计软件执行单向方差分析:
如何在 Excel 中执行单向方差分析
如何在 R 中执行单向方差分析
如何在 Python 中执行单向方差分析
如何在 SAS 中执行单向方差分析
如何在 SPSS 中执行单向方差分析
如何在 Stata 中进行单向方差分析
如何在 TI-84 计算器上执行单向方差分析
在线单向方差分析计算器