如何在 stata 中进行单向方差分析
单向方差分析用于确定三个或更多独立组的平均值之间是否存在统计显着差异。
这种类型的检验称为单向方差分析,因为我们分析预测变量对响应变量的影响。如果我们对两个预测变量对响应变量的影响感兴趣,我们可以执行双向方差分析。
本教程介绍如何在 Stata 中执行单向方差分析。
示例:Stata 中的单向方差分析
在此示例中,我们将使用名为systolic的内置 Stata 数据集来执行单向方差分析。该数据集包含 58 个不同个体的以下三个变量:
- 使用的药物
- 病人患病
- 收缩压的变化
我们将使用以下步骤进行单向方差分析,以确定所用药物类型是否会对收缩压变化产生显着影响。
第 1 步:加载数据。
首先,通过在命令框中键入webuse systolic并单击 Enter 来加载数据。
步骤2:查看原始数据。
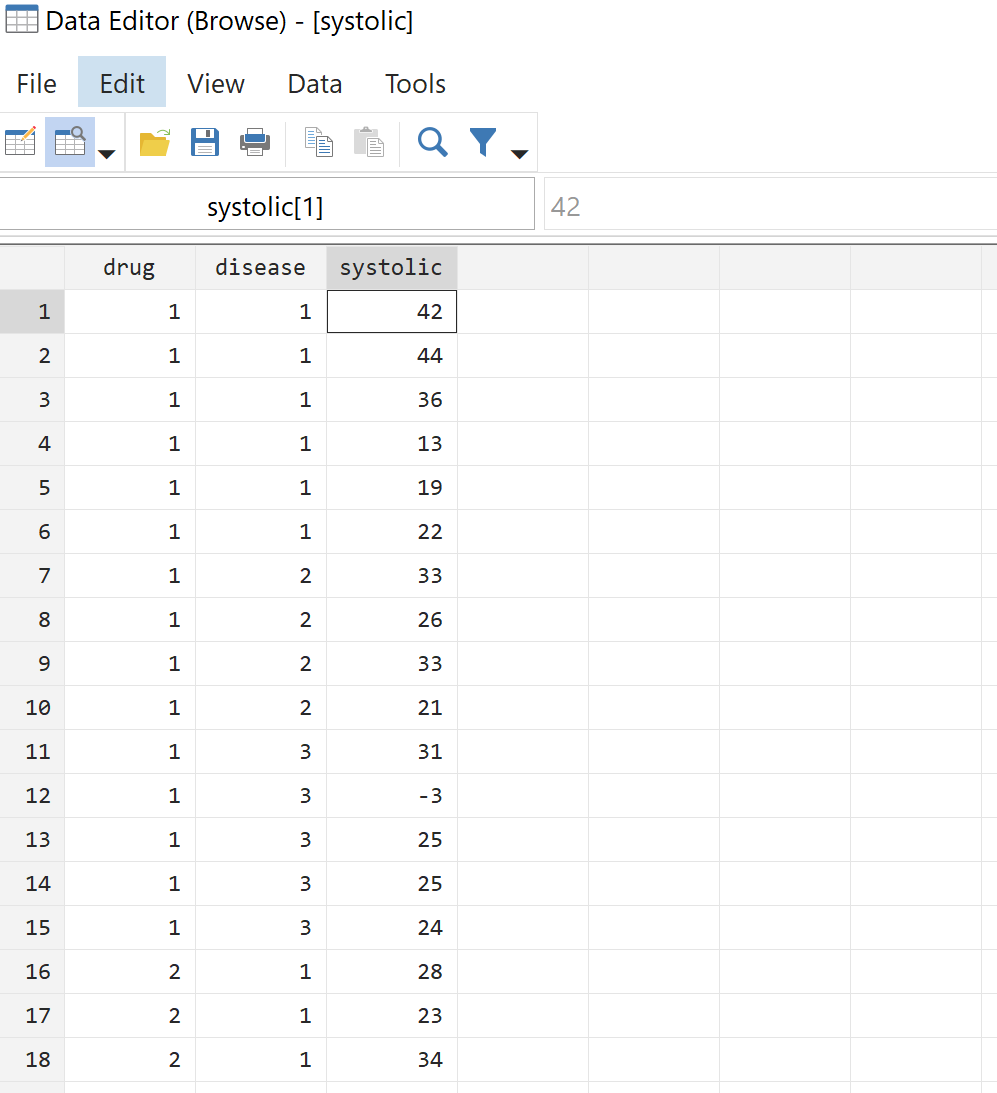
在执行单向方差分析之前,我们首先看一下原始数据。从顶部菜单栏中,导航至数据 > 数据编辑器 > 数据编辑器(浏览) 。这将向我们显示所有 58 名患者的实际数据:
第 3 步:可视化数据。
接下来,让我们可视化数据。我们将创建箱线图来显示每个药物类别的收缩压值的分布。
从顶部菜单栏中,转到图表 > 箱形图。在变量下,选择收缩压:
然后,在分组变量下的类别子标题中,选择药物:
单击“确定” 。将自动显示带有四个箱线图的图表:
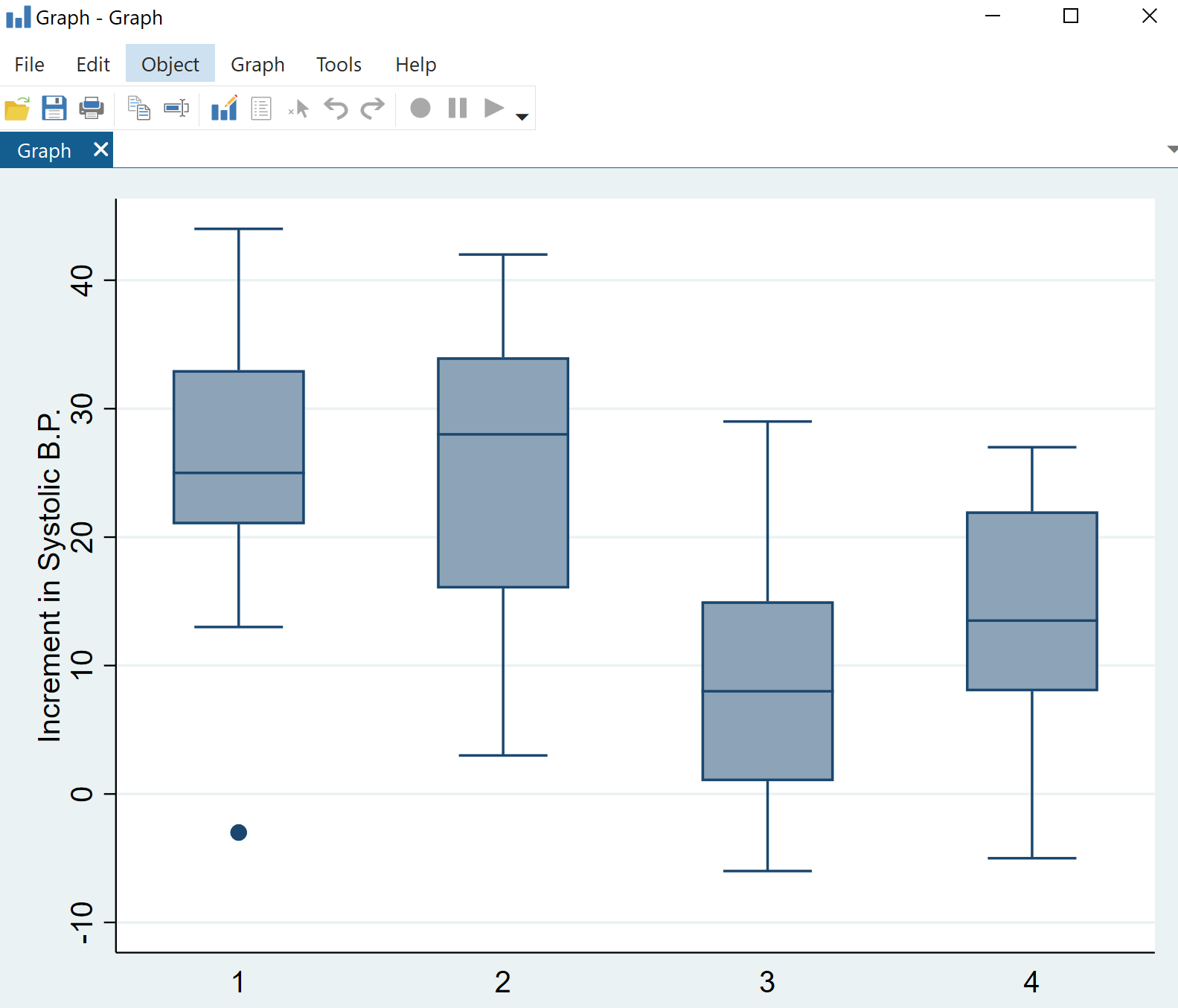
我们可以立即看到收缩压变化的分布因药物类别而异,但单向方差分析将告诉我们这些差异是否具有统计显着性。
第 4 步:执行单向方差分析。
从顶部菜单栏,导航至统计 > 线性和相关模型 > 方差分析/多元方差分析 > 单向方差分析。
在响应变量下,选择收缩压。在因素变量下,选择药物。然后单击“生成汇总表”旁边的框,以便我们可以看到每个组的一些基本描述性统计数据。然后单击“确定” 。
将显示以下输出:
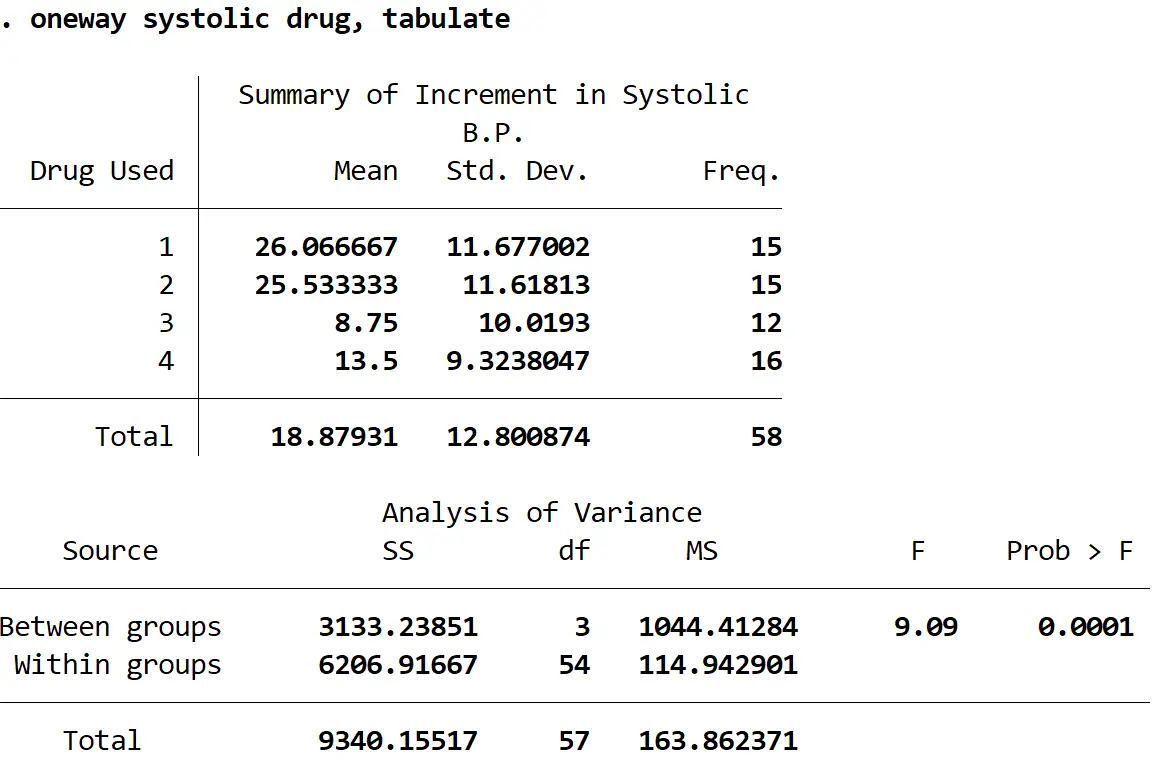
F 统计量为9.09 ,相应的 p 值为0.0001 。由于 p 值小于 alpha = 0.05,我们可以拒绝每组收缩压平均变化相等的原假设。
换句话说,至少两个药物组之间的收缩压平均变化存在统计学上的显着差异。
步骤5:进行多重比较测试。
然后我们可以运行几次比较测试来实际找出哪些组的平均值彼此不同。
从顶部菜单栏,导航至统计 > 摘要、表格和检验 > 摘要和描述性统计 > 均值配对比较。
对于变量,选择收缩响应变量。对于 Over,选择解释变量drug 。对于多重比较调整,选择Tukey 方法。
然后,在“报告”子标题下,单击“效应表”旁边的按钮,并选中“显示具有置信区间和 p 值的效应表”旁边的框。然后单击“确定” 。
将显示以下结果:
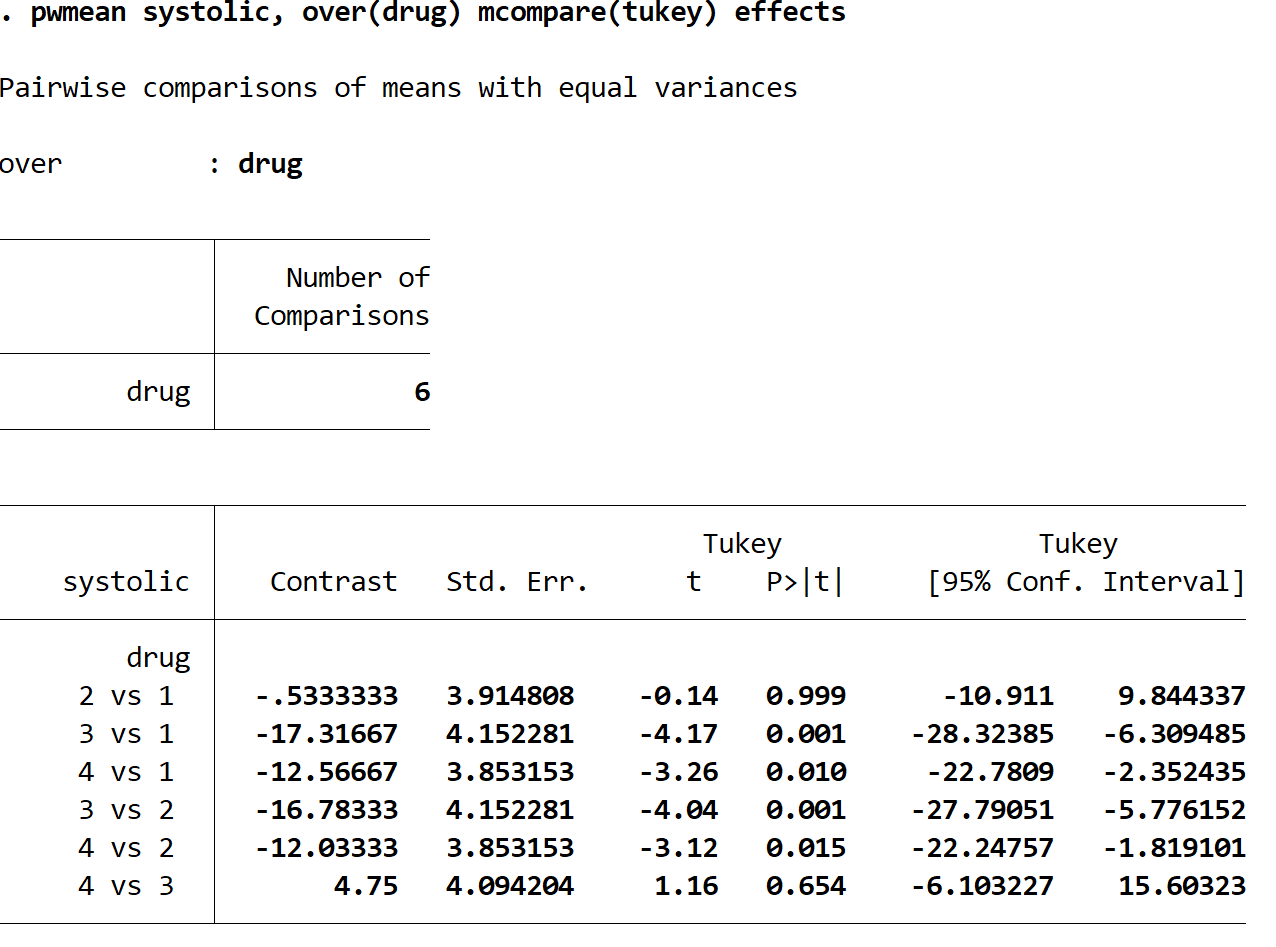
每行代表两个特定药物组之间的比较。例如,第一行比较药物组 2 和药物组 1 之间收缩压的平均变化。此比较的 p 值为0.999 ,该值非常高且不小于 0.05。这意味着药物组 1 和药物组 2 之间不存在统计学上的显着差异。
然而,我们可以看到以下比较的p值均小于0.05:
- 医药3对1 | p 值 = 0.001
- 医药4对1 | p 值 = 0.010
- 药3对2 | p 值 = 0.001
- 药4对2 | p 值 = 0.015
这意味着各组之间收缩压平均变化的差异具有统计学意义。
第6步:报告结果。
最后,我们将报告单向方差分析的结果。以下是如何执行此操作的示例:
进行单向方差分析以确定四种不同类型的药物是否对收缩压有不同的影响。
下表总结了每组的参与者人数以及每组收缩压的平均变化和收缩压的标准差:
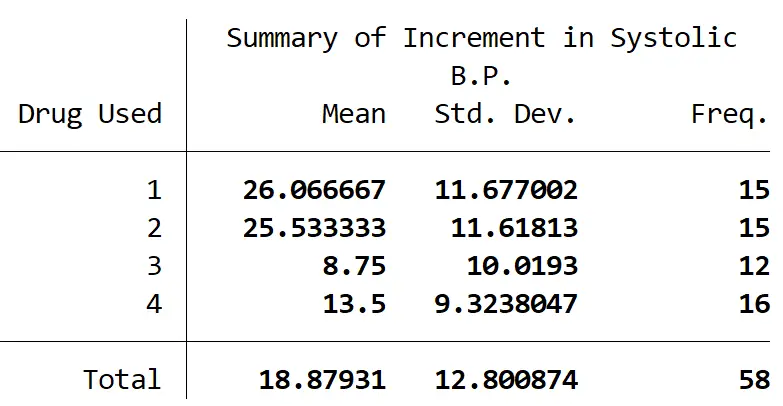
单向方差分析显示,至少两组之间存在统计学显着差异 (F(3, 54) = 9.09,p = 0.001)。
Tukey 多重比较检验显示,药物 3 的收缩压变化在统计学上显着高于药物 1 (17.32 +/- 4.15,p = 0.001),药物 3 的收缩压变化显着高于药物 2 (16.78 +/- 4.15, p = 0.001),药物 4 与药物 1 相比(12.57 +/- 3.85,p = 0.010),药物 4 与药物 2 相比(12.03 +/- 3.85,p = 0.015)。
药物组 1 和 2 之间(0.533 +/- 3.91,p = 0.999)或药物组 3 和 4 之间(4.75 +/- 4.09,p = 0.654)之间没有统计学显着差异。