卡方分布

经过本杰明·安德森博 8月 4, 2023 可能性 0 条评论

本文解释什么是卡方分布及其用途。此外，您还将找到卡方分布图及其属性。

什么是卡方分布？

卡方分布是一种概率分布，其符号为 χ2。更准确地说，卡方分布是k 个服从正态分布的独立随机变量的平方和。

因此，卡方分布有k 个自由度。因此，卡方分布的自由度与其所代表的正态分布变量的平方和一样多。

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

卡方分布也称为皮尔逊分布。

应该注意的是，卡方分布是伽玛分布的特例。

卡方分布广泛用于统计推断，例如假设检验和置信区间。下面我们将看到这种概率分布有哪些应用。

卡方分布图

一旦我们了解了卡方分布的定义，我们就会看到以图形方式表示的此类分布的几个示例。因此，您可以在下面看到卡方分布的概率图如何根据自由度变化。

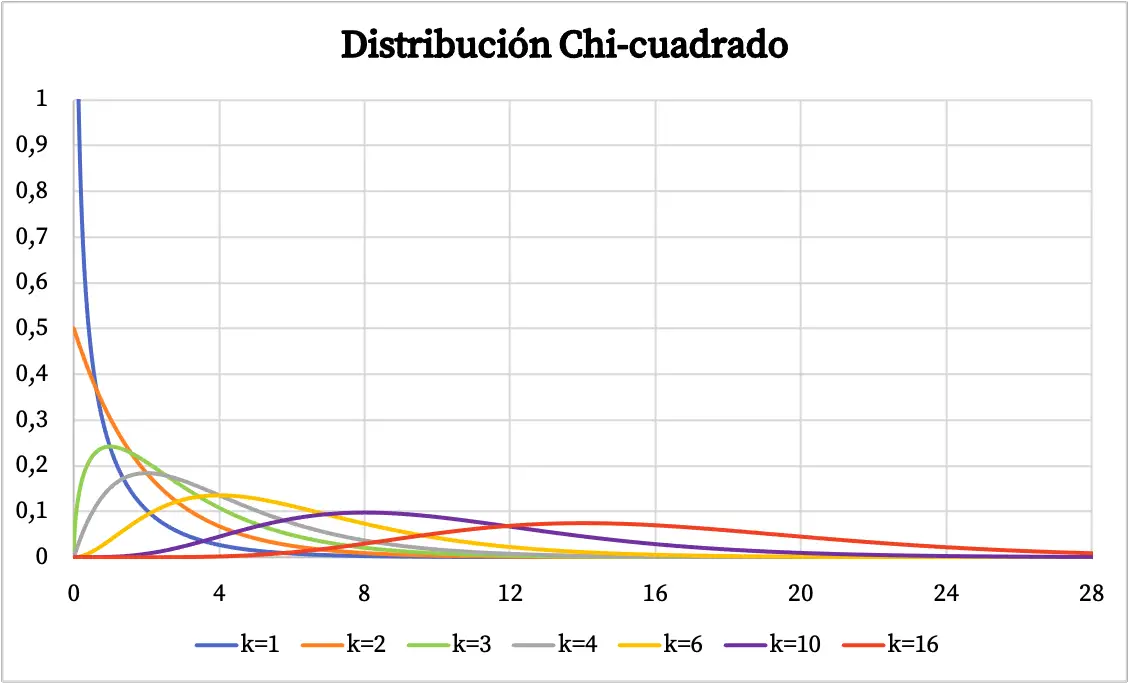
上图描述了卡方分布的密度函数。另一方面，卡方累积概率分布函数的图形如下：

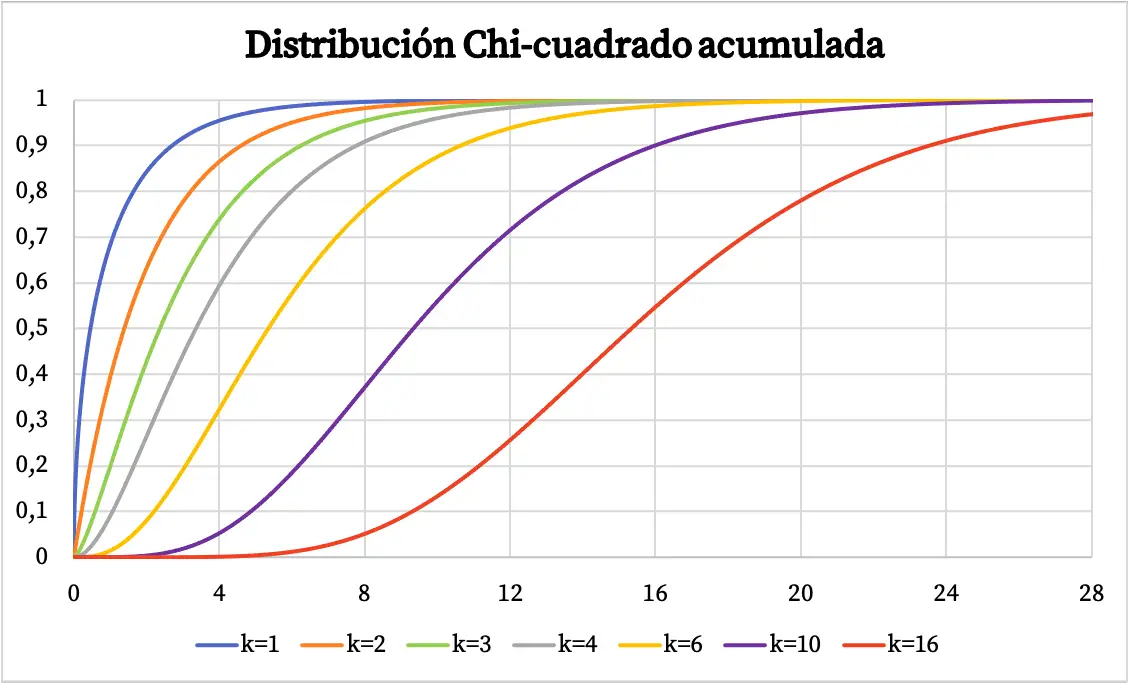
➤参见：卡方分布表

卡方分布的特征

在本节中，我们将看到与概率论和统计学相关的卡方分布的最重要属性。

卡方分布的平均值等于其自由度。

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

卡方分布的方差等于分布自由度的两倍。

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

只要分布具有多个自由度，卡方分布的众数就比其自由度小两个单位。

$Mo=k-2 \qquad \text{si } k\geq 2$

如果 x=0，卡方分布的密度函数为零。然而，对于大于 0 的 x 值，卡方分布的密度函数由以下公式定义：

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

卡方分布的累积分布函数由以下公式控制：

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

卡方分布的偏度系数是八除以分布自由度数所得的商的平方根。

$\displaystyle A=\sqrt{\frac{8}{k}}$

卡方分布的峰度使用以下表达式计算：

$C=3+\cfrac{12}{k}$

根据中心极限定理，如果k足够大，卡方分布可以近似为正态分布。

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

卡方分布的应用

卡方分布在统计学中有许多不同的应用。事实上，甚至还有卡方检验，用于检查变量之间的独立性以及理论分布的拟合优度。例如，卡方检验可用于确定样本数据是否符合泊松分布。

在线性回归分析中，卡方分布还用于估计正态分布总体的平均值以及估计线性回归研究线的斜率。

最后，卡方分布还通过其与 Snedecor F 分布的关系参与方差分析。

关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多