回归或分类:有什么区别?
机器学习算法可以分为两种不同的类型: 监督学习算法和无监督学习算法。
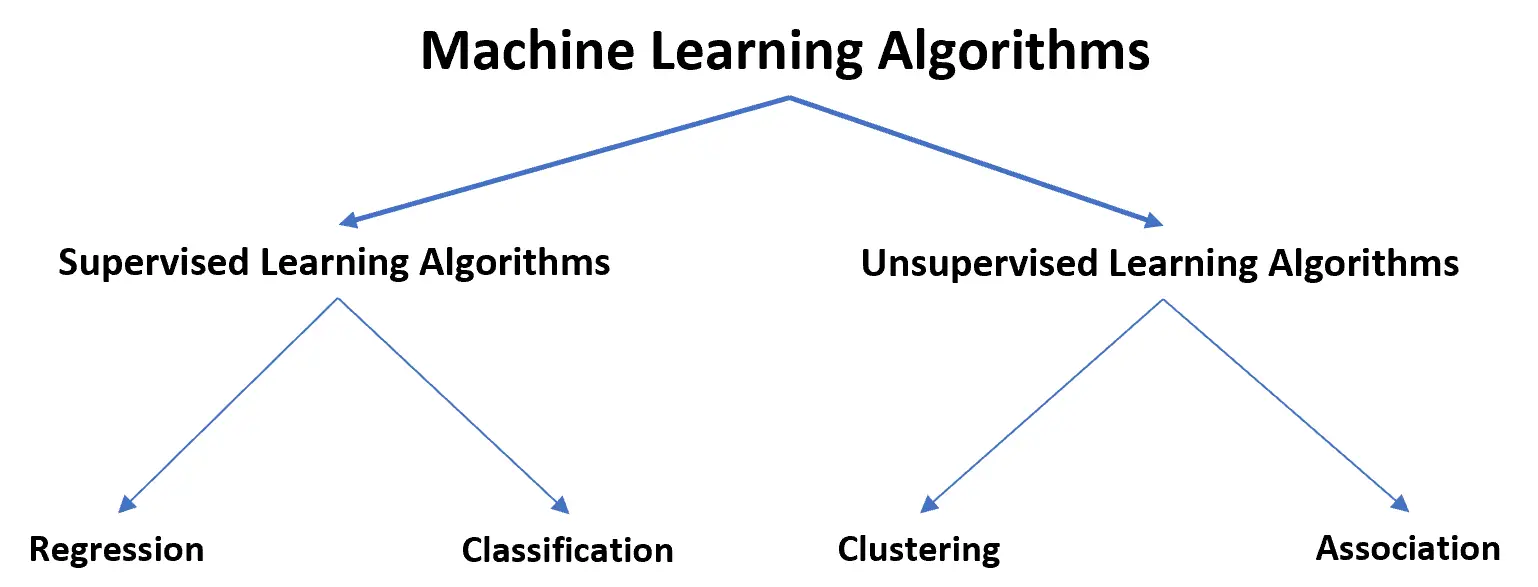
监督学习算法可以分为两类:
1.回归:响应变量是连续的。
例如, 响应变量可以是:
- 重量
- 高度
- 价格
- 时间
- 总单位数
在每种情况下,回归模型都会寻求预测连续量。
回归示例:
假设我们有一个数据集,其中包含 100 个不同房屋的三个变量:平方英尺、浴室数量和销售价格。
我们可以拟合一个回归模型,使用平方英尺和浴室数量作为解释变量,销售价格作为响应变量。
然后,我们可以使用该模型根据房屋的面积和浴室数量来预测房屋的售价。
这是回归模型的示例,因为响应变量(销售价格)是连续的。
衡量回归模型准确性的最常见方法是计算均方根误差 (RMSE),该指标告诉我们模型中的预测值与观测值的平均差距有多大。计算方法如下:
RMSE = √ Σ(P i – O i ) 2 / n
金子:
- Σ 是一个奇特的符号,意思是“和”
- P i是第 i 个观测值的预测值
- O i是第 i 个观测值的观测值
- n 是样本量
RMSE 越小,回归模型就越能拟合数据。
2. 分类:响应变量是分类的。
例如,响应变量可以采用以下值:
- 男女不限
- 成功或失败
- 低、中或高
在每种情况下,分类模型都会尝试预测类别标签。
分类示例:
假设我们有一个数据集,其中包含 100 名不同大学篮球运动员的三个变量:场均得分、分区级别以及他们是否被选入 NBA。
我们可以采用一个分类模型,使用每场比赛和每个级别的平均得分作为解释变量,并使用“起草”作为响应变量。
然后,我们可以使用该模型根据特定球员的场均得分和分区级别来预测该球员是否会被选入 NBA。
这是分类模型的示例,因为响应变量(“书面”)是分类的。换句话说,它只能取两个不同类别的值:“书面”或“未起草”。
衡量分类模型准确性的最常见方法就是计算模型正确分类的百分比:
准确率 = 校正分类数 / 分类尝试总数 * 100%
例如,如果模型在可能的 100 次中正确识别一名球员是否会被选入 NBA 88 次,则该模型的准确度为:
准确度 = (88/100) * 100% = 88%
准确度越高,分类模型预测结果的能力就越好。
回归和分类之间的相似之处
回归和分类算法在以下方面相似:
- 两者都是监督学习算法,也就是说,它们都涉及响应变量。
- 两者都使用一个或多个解释变量来创建模型来预测响应。
- 两者都可以用来理解解释变量值的变化如何影响响应变量的值。
回归和分类之间的差异
回归和分类算法在以下方面有所不同:
- 回归算法寻求预测连续量,而分类算法寻求预测类别标签。
- 我们衡量回归模型和分类模型准确性的方式不同。
将回归转换为分类
应该注意的是,通过简单地将响应变量离散成区间,可以将回归问题转换为分类问题。
例如,假设我们有一个包含三个变量的数据集:平方英尺、浴室数量和销售价格。
我们可以使用平方英尺和浴室数量构建回归模型来预测销售价格。
但是,我们可以将销售价格离散为三个不同的类别:
- $80,000 – $160,000:“低价”
- 161,000 美元 – 240,000 美元:“平均售价”
- 241,000 美元 – 320,000 美元:“高售价”
然后,我们可以使用平方英尺和浴室数量作为解释变量来预测给定房屋的销售价格将属于哪个类别(低、中或高)。
这将是分类模型的一个示例,因为我们试图将每个房子放入一个类中。
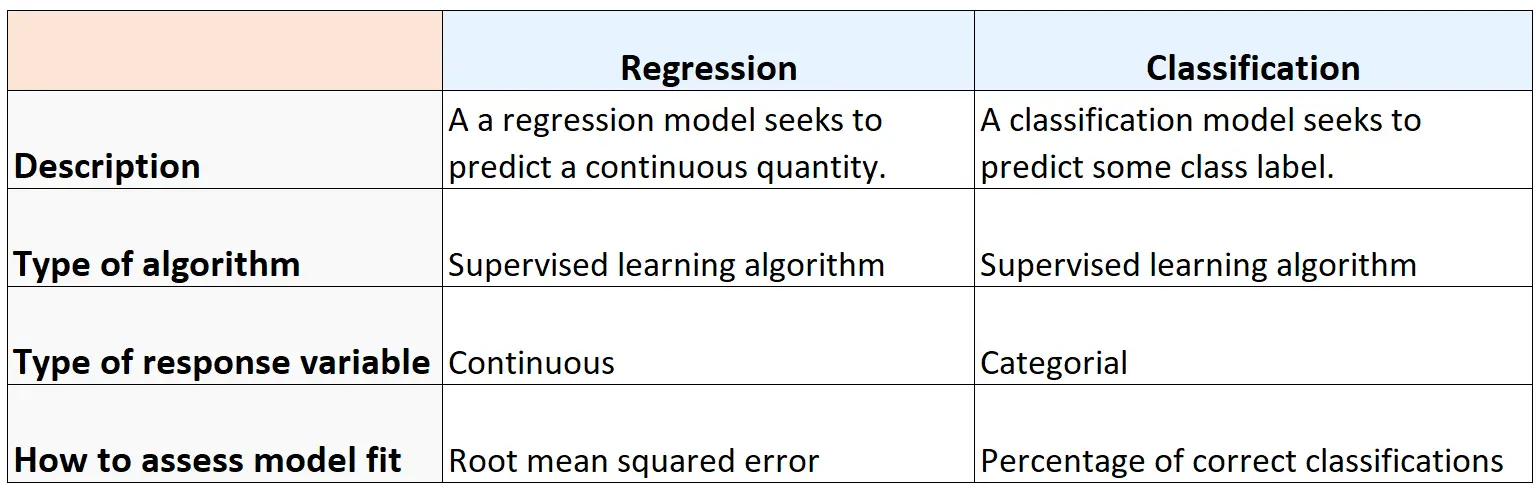
概括
下表总结了回归算法和分类算法之间的异同: