均值差异的置信区间
本文解释了统计学中均值差异的置信区间是什么及其用途。因此,您将了解如何计算两个均值之差的置信区间以及逐步解决的练习。
均值差异的置信区间是多少?
均值差的置信区间是提供最大值和最小值的区间,在该最大值和最小值之间,两个总体的均值差值具有一定的置信水平。
例如,如果置信水平为 95% 的两个总体均值差异的置信区间为 (3.5),则这意味着两个总体均值之间的差异将在 3 到 5 之间,概率为 95 %。
因此,在统计学中,均值差异的置信区间用于估计两个总体均值之间的差异所在的两个值。因此,使用来自两个样本的数据,可以近似估计总体平均值之间的差异。
均值差异的置信区间公式
均值差异的置信区间公式取决于总体方差是否已知,如果未知,则是否可以假定总体方差相等。 。然后我们将了解在每种情况下如何计算均值差异的置信区间。
已知偏差
当两个总体的方差已知且置信水平为 1-α 时,计算均值差的置信区间的公式如下:
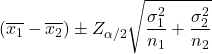
金子:
-

是样本 i 的平均值。
-

是总体 i 的标准差。
-

是概率为 α/2 的标准正态分布的值。
-

是样本大小 i。
这种情况是最不常见的,因为总体方差的值通常是未知的。
未知且等方差
当两个总体的方差未知但可以估计相等时,置信水平为1-α的均值之差的置信区间计算公式如下:
![]()
金子:
-

是样本 i 的平均值。
-

是汇总标准差。
-

是 n 1 + n 2 -2 自由度的 Student t 分布值,概率为 α/2。
-

是样本大小 i。
由于在这种情况下假设总体方差相等,因此使用组合标准差来计算置信区间,其计算公式如下:

金子
![]()
是样本 i 的标准差。
未知和不同的变化
当两个总体的方差未知且不能假设相等时,置信水平为1-α的均值之差的置信区间计算公式如下:
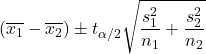
金子:
-

是样本 i 的平均值。
-
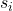
是样本 i 的标准差。
-

是概率为 α/2 的 Student t 分布的值。
-

是样本大小 i。
在这种情况下,Student t 分布的自由度使用以下公式计算:

金子
![]()
是样本 i 的标准差。
均值差异置信区间的具体示例
在了解了均值差的置信区间的定义以及不同的公式是什么之后,我们现在将看到一个具体的示例来完成如何计算两个均值差的置信区间。
- 我们想研究烟草对儿童出生体重的影响。为此,需要比较两个样本:第一个样本由母亲不吸烟的儿童组成,第二个样本由母亲吸烟的儿童组成(样本参数如下所示)。计算置信水平为 95% 的均值差异的置信区间。
- 不吸烟的妈妈们:
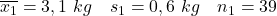
- 吸烟的妈妈们:
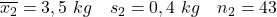
- 不吸烟的妈妈们:
在这种情况下,我们不知道总体方差的值,但是,我们可以假设总体方差是相等的,因为我们正在处理两个具有非常相似特征的总体。因此,我们应该使用均值差异的置信区间公式为:
![]()
因此,我们根据两个样本的标准差计算组合标准差:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
同样,我们必须在 Student t 分布的概率分布表中找到 80 自由度的 Student t 分布,概率为 2.5% 的值:
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
最后,我们将数据代入均值差的置信区间公式中并进行计算:
![]()
![]()
![]()
因此,问题均值差异的置信区间如下:
![]()