多元线性回归的五个假设

多元线性回归是一种统计方法，我们可以用它来理解多个预测变量和响应变量之间的关系。

然而，在进行多元线性回归之前，我们必须首先确保满足五个假设：

1.线性关系：各预测变量与响应变量之间存在线性关系。

2. 不存在多重共线性：预测变量之间没有高度相关。

3. 独立性：观察结果是独立的。

4.同方差性：残差在线性模型的每个点上具有恒定的方差。

5.多元正态性：模型残差呈正态分布。

如果不满足这些假设中的一个或多个，则多元线性回归的结果可能不可靠。

在本文中，我们对每个假设进行了解释，如何确定假设是否满足，以及如果不满足假设该怎么办。

假设1：线性关系

多元线性回归假设每个预测变量和响应变量之间存在线性关系。

如何确定这个假设是否满足

确定是否满足此假设的最简单方法是创建每个预测变量和响应变量的散点图。

这使您可以直观地看到两个变量之间是否存在线性关系。

如果散点图中的点大致沿着直线对角线分布，则变量之间可能存在线性关系。

例如，下图中的点似乎落在一条直线上，表明该特定预测变量 (x) 和响应变量 (y) 之间存在线性关系：

如果不遵守此假设该怎么办

如果一个或多个预测变量与响应变量之间不存在线性关系，那么我们有以下几种选择：

1.对预测变量应用非线性变换，例如取对数或平方根。这通常可以使关系变得更加线性。

2.将另一个预测变量添加到模型中。例如，如果 x 与 y 的图具有抛物线形状，则在模型中添加 X ²作为附加预测变量可能是有意义的。

3.从模型中删除预测变量。在最极端的情况下，如果某个预测变量与响应变量之间不存在线性关系，则在模型中包含该预测变量可能没有用。

假设2：不存在多重共线性

多元线性回归假设没有一个预测变量彼此高度相关。

当一个或多个预测变量高度相关时，回归模型会出现多重共线性，从而导致模型的系数估计不可靠。

如何确定这个假设是否满足

确定是否满足此假设的最简单方法是计算每个预测变量的 VIF 值。

VIF值从1开始，没有上限。一般来说，VIF值高于5*表明存在潜在的多重共线性。

以下教程展示了如何在各种统计软件中计算VIF：

• 如何在R中计算VIF
• 如何用Python计算VIF
• 如何在Excel中计算VIF

*有时研究人员会使用 VIF 值 10，具体取决于研究领域。

如果不遵守此假设该怎么办

如果一个或多个预测变量的 VIF 值大于 5，则解决此问题的最简单方法是删除具有高 VIF 值的预测变量。

或者，如果您希望将每个预测变量保留在模型中，则可以使用不同的统计方法，例如岭回归、套索回归或偏最小二乘回归，旨在处理高度相关的预测变量。

假设3：独立性

多元线性回归假设数据集中的每个观测值都是独立的。

如何确定这个假设是否满足

确定是否满足此假设的最简单方法是执行Durbin-Watson 检验，这是一种正式的统计检验，可以告诉我们残差（以及观测值）是否表现出自相关。

如果不遵守此假设该怎么办

根据违反此假设的方式，您有多种选择：

• 对于正序列相关，请考虑向模型添加因变量和/或自变量的滞后。
• 对于负序列相关，请确保没有任何变量过度延迟。
• 对于季节性相关性，请考虑向模型添加季节性虚拟变量。

假设4：同方差性

多元线性回归假设线性模型中每个点的残差具有恒定方差。如果情况并非如此，残差就会出现异方差。

当回归分析中存在异方差时，回归模型的结果变得不可靠。

具体来说，异方差增加了回归系数估计值的方差，但回归模型并未考虑到这一点。这使得回归模型更有可能声称模型中的某个项具有统计显着性，而实际上并非如此。

如何确定这个假设是否满足

确定是否满足此假设的最简单方法是创建标准化残差与预测值的关系图。

将回归模型拟合到数据集后，您可以创建一个散点图，该散点图在 x 轴上显示响应变量的预测值，在 x 轴上显示模型的标准化残差。 y。

如果散点图中的点呈现趋势，则存在异方差性。

下图显示了一个回归模型的示例，其中异方差性不是问题：

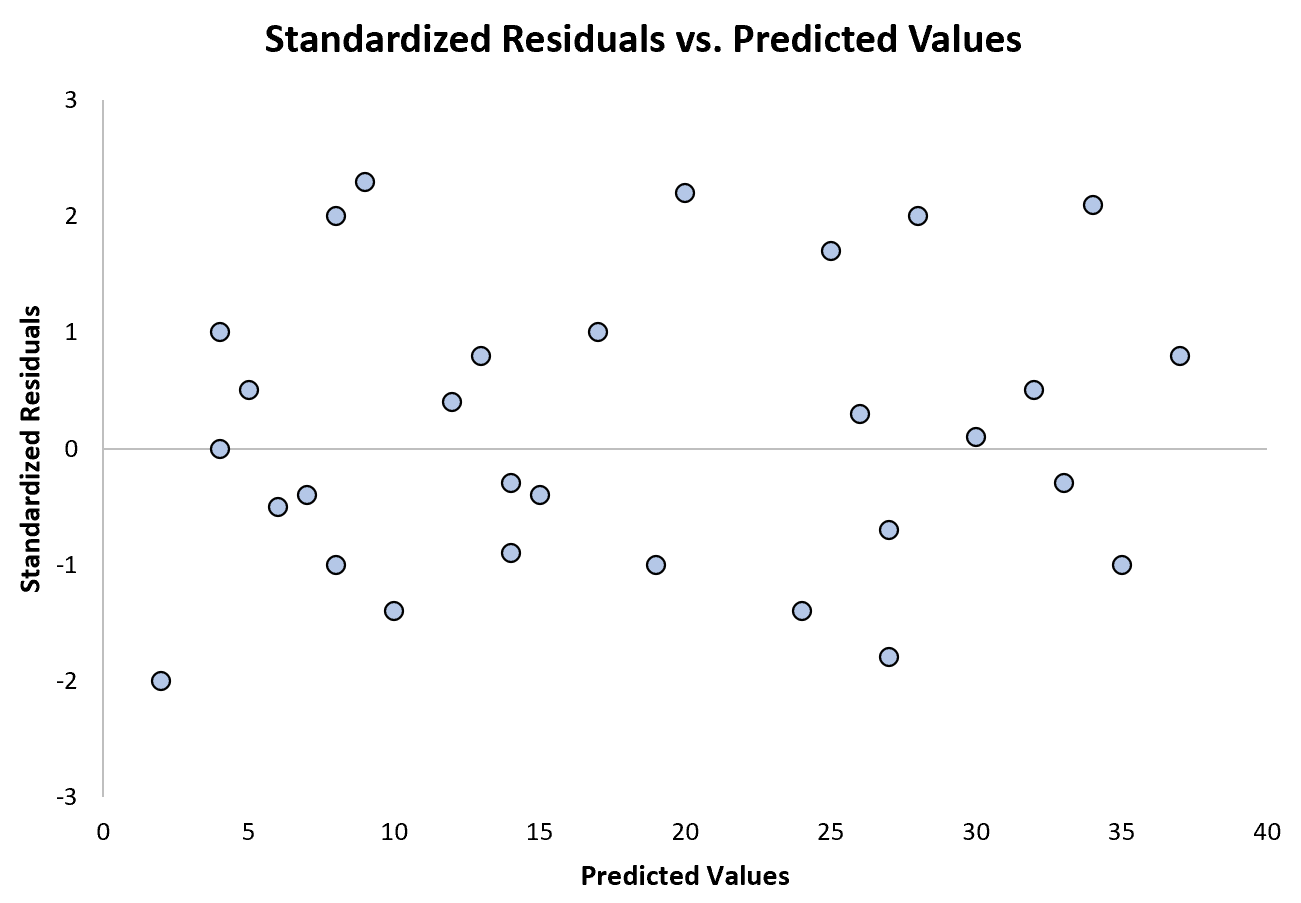
请注意，标准化残差分散在零附近，没有清晰的模式。

下图显示了存在异方差问题的回归模型示例：

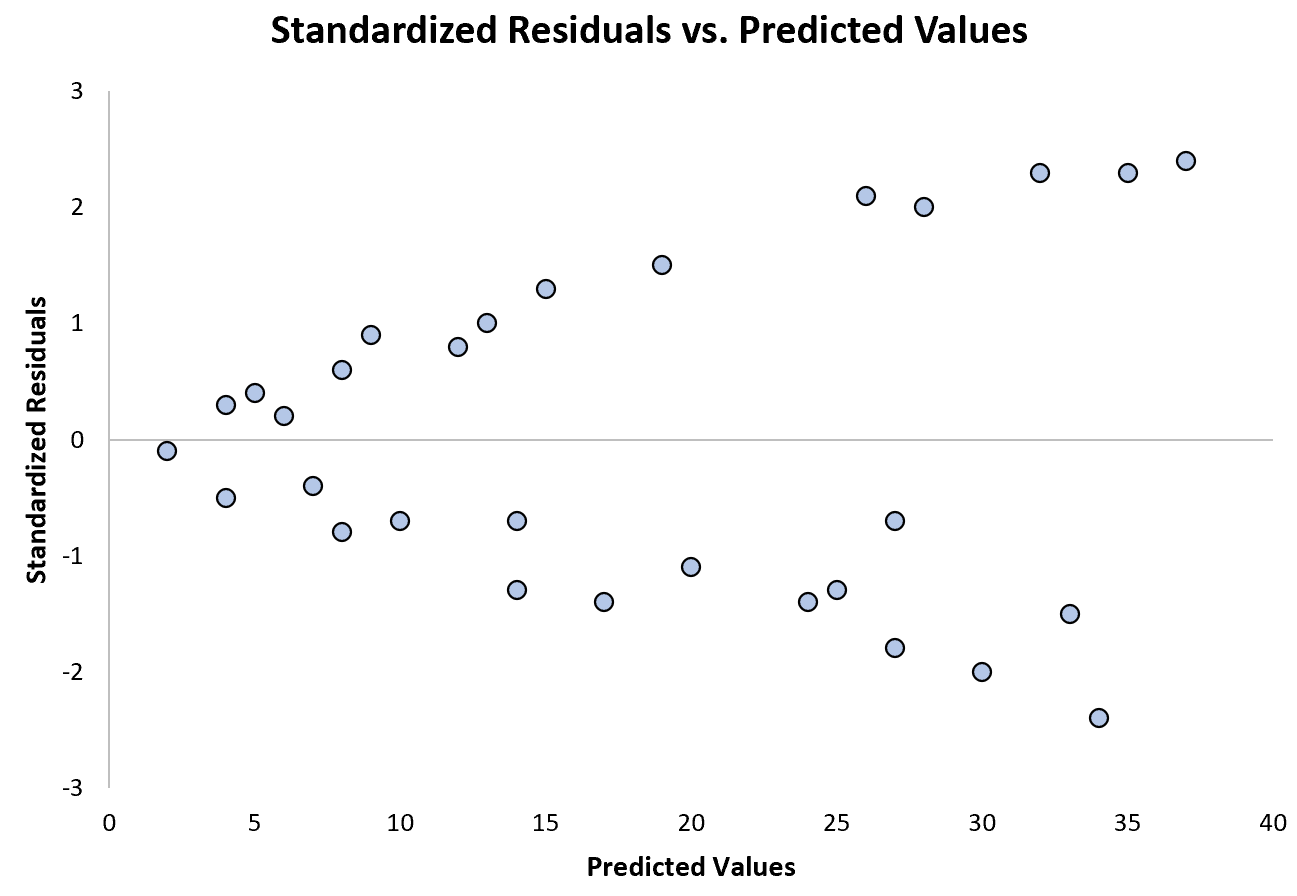
请注意，随着预测值的增加，标准化残差如何越来越分散。这种“圆锥”形状是异方差的典型标志：

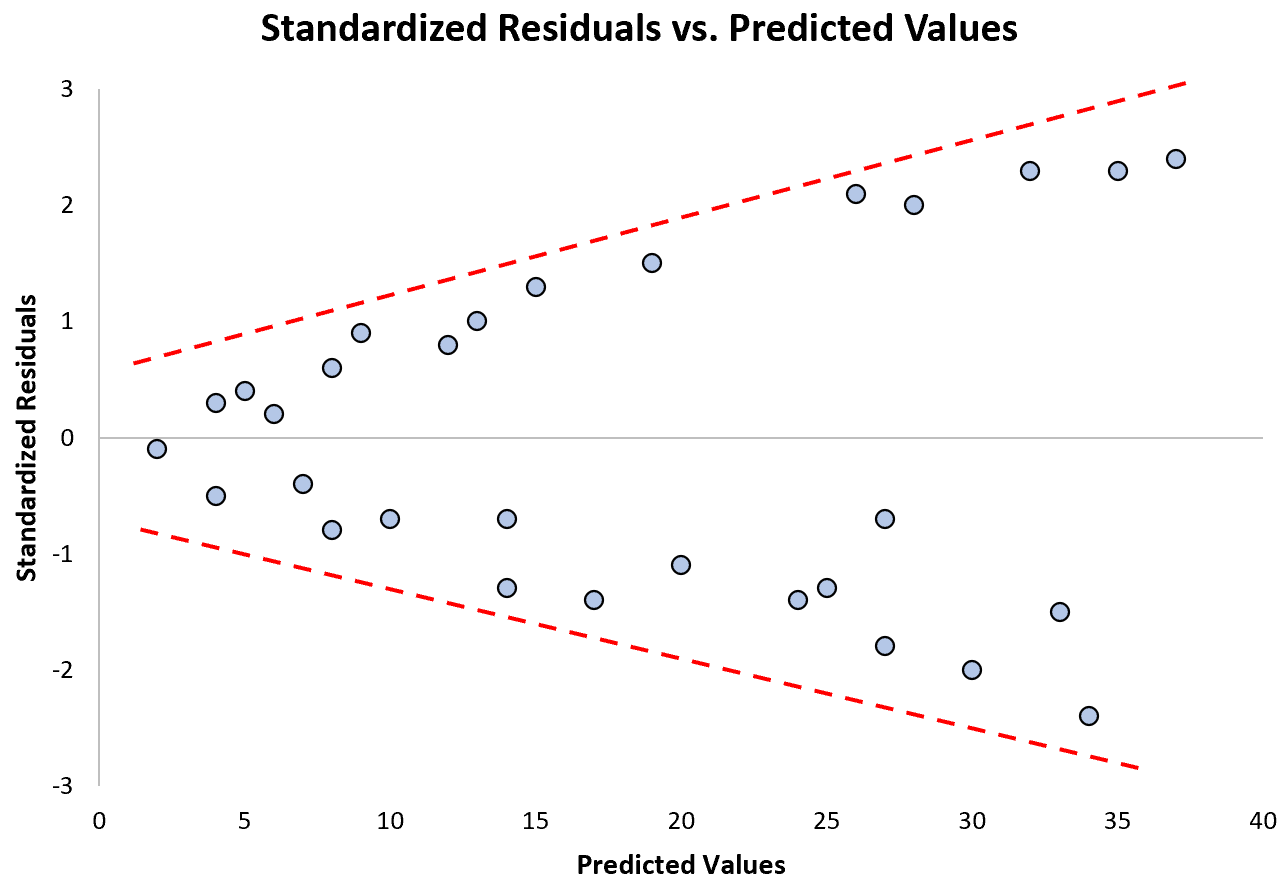
如果不遵守此假设该怎么办

校正异方差的常用方法有以下三种：

1. 变换响应变量。处理异方差最常见的方法是通过对响应变量的所有值取对数、平方根或立方根来变换响应变量。这通常会导致异方差消失。

2. 重新定义响应变量。重新定义响应变量的一种方法是使用比率而不是原始值。例如，我们可以使用人口规模来预测人均花店数量，而不是使用人口规模来预测一个城市的花店数量。

在大多数情况下，这减少了较大人群中自然发生的变异性，因为我们测量的是每人的花店数量，而不是花店本身的数量。

3. 使用加权回归。校正异方差的另一种方法是使用加权回归，它根据拟合值的方差为每个数据点分配权重。

本质上，这为具有较高方差的数据点赋予了较低的权重，从而减少了它们的残差平方。当使用适当的权重时，可以消除异方差问题。

相关： 如何在 R 中执行加权回归

假设 4：多元正态性

多元线性回归假设模型残差呈正态分布。

如何确定这个假设是否满足

有两种常见的方法来检查这个假设是否满足：

1. 使用QQ 图直观地验证假设。

QQ 图是分位数-分位数图的缩写，是一种图，我们可以用它来确定模型的残差是否服从正态分布。如果图上的点大致形成一条直线对角线，则满足正态性假设。

下面的 QQ 图显示了一个大致服从正态分布的残差示例：

然而，下面的 QQ 图显示了残差明显偏离直线对角线的情况示例，表明它们不服从正态分布：

2.使用正式的统计检验（例如 Shapiro-Wilk、Kolmogorov-Smironov、Jarque-Barre 或 D’Agostino-Pearson）验证假设。

请记住，这些检验对大样本量很敏感 – 也就是说，当样本量极大时，它们通常会得出残差不正常的结论。这就是为什么使用 QQ 图等图形方法通常更容易验证这一假设。

如果不遵守此假设该怎么办

如果不满足正态性假设，您有多种选择：

1.首先，检查数据中是否存在导致违反正态性假设的极端异常值。

2.然后您可以对响应变量应用非线性变换，例如对响应变量的所有值求平方根、对数或立方根。这通常会导致模型残差更加正态分布。

其他资源

以下教程提供有关多元线性回归及其假设的更多信息：

多元线性回归简介
回归分析中的异方差指南
回归中的多重共线性和 VIF 指南

以下教程提供了有关如何使用不同统计软件执行多元线性回归的分步示例：

如何在 Excel 中执行多元线性回归
如何在 R 中执行多元线性回归
如何在 SPSS 中执行多元线性回归
如何在Stata中进行多元线性回归