如何解释 mape 值

衡量模型预测准确性的最常用指标之一是平均绝对百分比误差，通常缩写为MAPE 。

计算方法如下：

MAPE = (1/n) * Σ(|实际 – 预测| / |实际|) * 100

金子：

• Σ – 表示“和”的符号
• n——样本量
• 实际——数据的真实价值
• Forecast——数据的预测值

MAPE 之所以常用是因为它很容易解释。例如，MAPE 值为 14% 表示预测值与实际值之间的平均差异为 14%。

以下示例显示如何计算和解释给定模型的 MAPE 值。

示例：解释给定模型的 MAPE 值

假设一家杂货连锁店正在构建一个模型来预测未来的销售。下图展示了该车型连续12个销售周期的实际销量和预测销量：

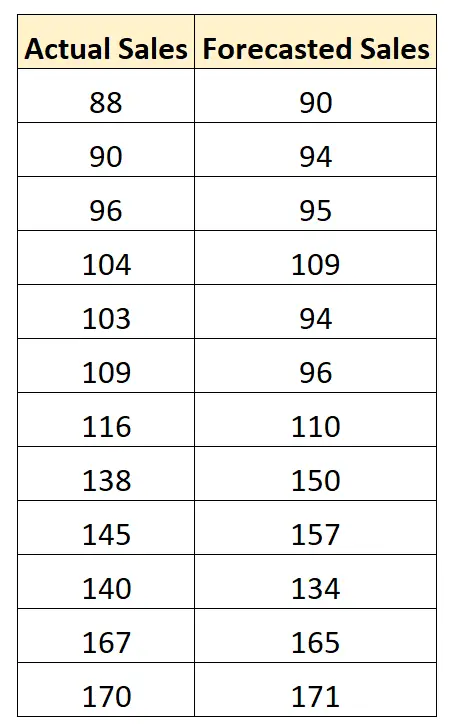
我们可以使用以下公式来计算每个预测的绝对百分比误差：

• 绝对误差百分比 = |实际预测| / |真实| *100

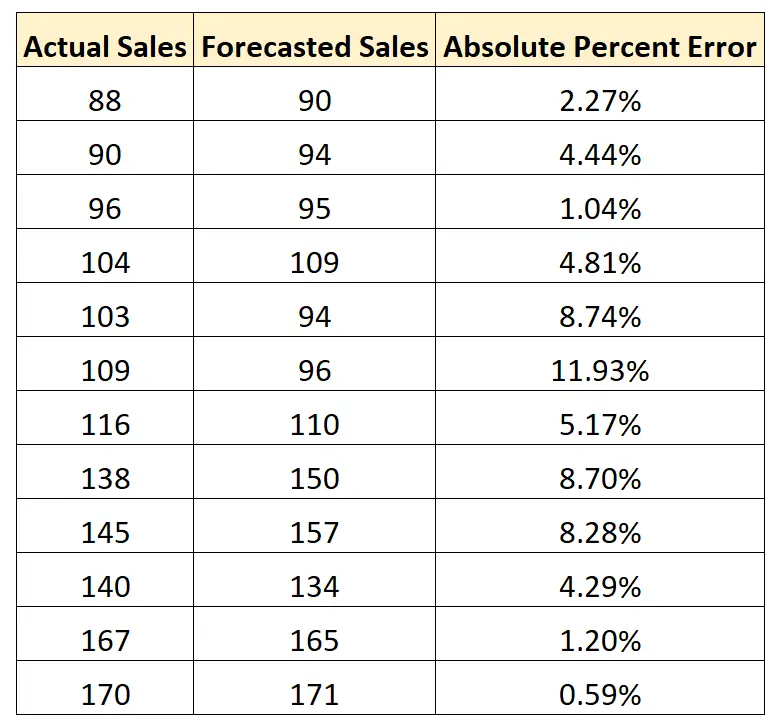
然后我们可以计算绝对误差百分比的平均值：

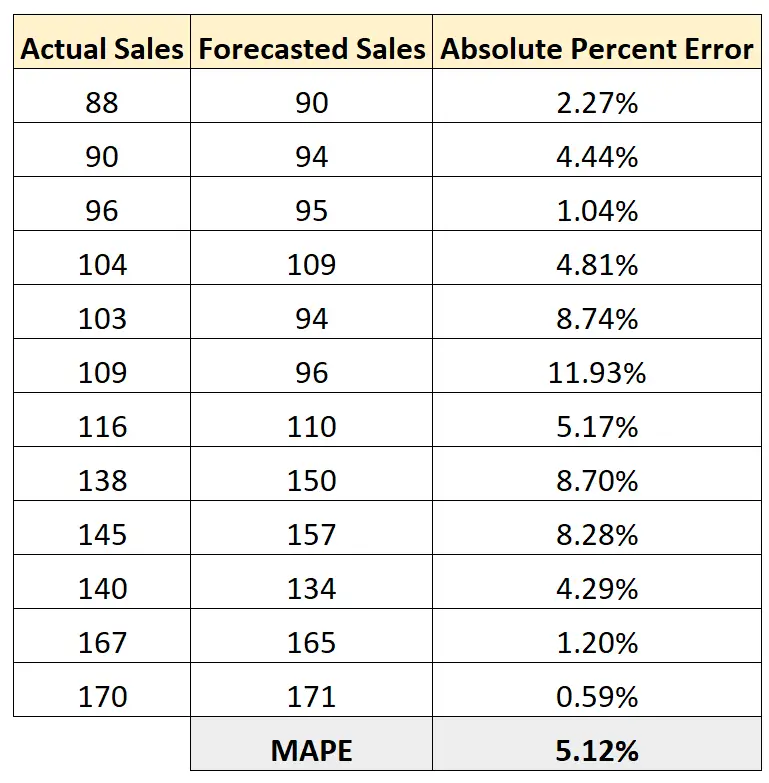
该模型的 MAPE 结果为5.12% 。

这告诉我们，模型预测销售额与实际销售额之间的平均绝对百分比误差为5.12% 。

确定这对于 MAPE 是否是一个好的值取决于行业标准。

如果标准食品工业生产模型的 MAPE 值为 2%，那么 5.12% 的值可以认为很高。

相反，如果大多数行业杂货预测模型产生的 MAPE 值在 10% 到 15% 之间，那么 5.12% 的 MAPE 值可以被认为较低，并且该模型可以被认为非常适合预测未来销售。

不同模型MAPE值对比

MAPE 对于比较不同模型的拟合度特别有用。

例如，假设一家杂货连锁店想要创建一个模型来预测未来的销售，并希望在多个潜在模型中找到最佳的模型。

假设它们匹配三个不同的模型并找到它们相应的 MAPE 值：

• 模型1的MAPE： 14.5%
• 模型 2 MAPE： 16.7%
• 模型 3 MAPE： 9.8%

Model 3 的 MAPE 值最低，这表明它在三种潜在模型中能够以最高的准确度预测未来销量。

其他资源

如何在 Excel 中计算 MAPE
如何在 R 中计算 MAPE
如何在Python中计算MAPE
MAPE计算器