平均值、中位数和众数

经过本杰明·安德森博 8月 5, 2023 统计数据 0 条评论

本文解释了什么是均值、中位数和众数。您将了解如何获取均值、中位数和众数、它们的用途以及这三种统计度量之间的差异。此外，您将能够使用最后的在线计算器计算任何统计样本的平均值、中位数和众数。

什么是平均值、中位数和众数？

平均值、中位数和众数是中心位置的统计度量。换句话说，均值、中位数和众数是帮助定义统计样本的值，特别是它们表明其中心值是什么。

平均值、中位数和众数定义如下：

平均值：是样本中所有数据的平均值。
中位数：这是所有数据从小到大排序的中间值。
众数：这是数据集中重复次数最多的值。

下面将更详细地解释这三种统计指标。

一半

要计算平均值，请将所有值相加，然后除以数据总数。因此，平均值的公式如下：

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}$

👉您可以使用下面的计算器计算任何数据集的平均值、中位数和众数。

平均符号是字母 x 上方的水平带

$(\overline{x}).$

您还可以使用均值符号区分样本均值和总体均值：样本均值用符号表示

$\overline{x}$

，而人口平均值则使用希腊字母

$\mu.$

平均值也称为算术平均值或平均数。此外，统计分布的平均值相当于其数学期望。

平均示例

学生在学年中取得以下成绩：数学 9 分、语言 7 分、历史 6 分、经济学 8 分、科学 7.5 分。你所有成绩的平均分是多少？

为了求算术平均数，我们需要将所有成绩相加，然后除以课程的科目总数，即 5。因此，我们应用算术平均数公式：

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}$

我们将数据代入公式并计算算术平均值：

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

可以看到，在算术平均中，对每个值赋予相同的权重，即每条数据在整体中具有相同的权重。

中位数

中位数是所有数据从小到大排序的中间值。换句话说，中位数将有序数据集分成相等的两部分。

中位数的计算取决于数据总数是偶数还是奇数：

如果数据总数为奇数，则中位数将是位于数据正中间的值。也就是说排序后的数据中位于(n+1)/2位置的值。

$Me=x_{\frac{n+1}{2}$

如果数据点总数为偶数，则中位数为位于中心的两个数据点的平均值。也就是说，在有序数据的 n/2 和 n/2+1 位置处找到的值的算术平均值。

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

金子

$n$

是样本中数据项的总数。

Me一词经常用作符号来表示某个值是所有观测值的中值。

👉您可以使用下面的计算器计算任何数据集的平均值、中位数和众数。

中位数示例

求以下数据的中位数：3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5

在进行计算之前首先要做的就是对数据进行分类，即我们将数字从小到大排列。

$1 \ 2 \ 3 \ 4 \ 4 \ 4 \ 5 \ 6 \ 7 \ 8 \ 8$

在本例中，我们有 11 个观测值，因此数据总数为奇数。因此，我们应用以下公式来计算中位数的位置：

$\cfrac{n+1}{2}=\cfrac{11+1}{2}=6$

因此，中位数将是位于第六位的数据，在本例中对应于值 4。

$Me=x_6=4$

时尚

在统计学中，众数是数据集中出现频率最高的值，即众数是数据集中重复次数最多的值。

因此，要计算统计数据集的众数，只需统计每个数据元素在样本中出现的次数，重复次数最多的数据就是众数。

众数也可以说是统计众数或众数。类似地，当数据按区间分组时，最重复的区间是模态区间或模态类别。

一般情况下，术语Mo用作统计模式的符号，例如分布模式X为Mo(X)。

根据最多重复值的数量可以区分三种模式：

单峰模式：只有一个值具有最大重复次数。例如，[1,4,2,4,5,3]。
双峰模式：最大重复次数出现在两个不同的值处，并且两个值重复的次数相同。例如，[2,6,7,2,3,6,9]。
多峰模式：三个或更多值具有相同的最大重复次数。例如，[3,3,4,1,3,4,2,1,4,5,2,1]。

👉您可以使用下面的计算器计算任何数据集的平均值、中位数和众数。

时尚范例

以下数据集的众数是什么？

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

这些数字是乱序的，所以我们要做的第一件事就是对它们进行排序。这一步不是强制性的，但它会帮助你更轻松地找到时尚。

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

数字 2 和 9 出现了两次，但数字 5 重复了 3 次。因此，数据序列的众数为5。

$Mo=5$

解决了均值、中位数和众数的练习

现在您已经知道平均值、中位数和众数是什么了，下面是对这些统计度量的详细练习，以便您可以准确地了解它们的计算方式。

求下列统计数据集的均值、中位数和众数：

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

为了求出数据的平均值，我们需要将它们全部相加，然后除以数据总数，即 30：

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}=\frac{192}{30}=6,4$

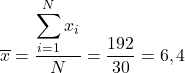
其次，让我们找出样本中位数。所以我们将所有数字按升序排列：

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

在这种情况下，数据总数是偶数，因此需要计算两个中心位置，在这两个中心位置之间找到中位数。为此，我们使用以下两个公式：

$\cfrac{n}{2}=\cfrac{30}{2}=15$

$\cfrac{n}{2}+1=\cfrac{30}{2}+1=16$

因此，中位数将位于第十五和第十六位置之间，分别对应于值 6 和 7。更准确地说，中位数相当于这些值的平均值：

$Me=\cfrac{x_{15}+x_{16}}{2}=\cfrac{6+7}{2}=6,5$

最后，要找到模式，您只需计算每个数字出现的所有次数即可。可以看到，数字6和数字8一共出现了四次，这是最大的重复次数。因此，在这种情况下它是双峰模式，两个数字是数据集的模式：

$Mo=\{ 6 \ ; \ 8\}$