平均类型（统计）

在这里，我们解释统计中所有类型的平均值以及它们的计算方法。您将找到每种类型的袜子的配方和示例。

但在了解平均值的类型之前，我们必须从逻辑上了解统计学中的平均值是什么。因此，我们建议您在继续之前先查阅以下链接。

统计中的平均值有哪些类型？

在统计学中，平均值的类型有：

• 算术平均
• 加权平均
• 几何平均值
• 均方根
• 和谐意义
• 广义平均数
• 广义 f 平均
• 修剪手段
• 四分位数平均值
• 函数的平均值

接下来我们将解释如何计算统计中所有类型的平均值。最常用的五种平均类型是算术平均、加权平均、几何平均、二次平均和调和平均。因此，我们将更详细地了解这五种主要媒体类型。

算术平均

算术平均值是通过将所有值相加然后除以数据点总数来计算的。

因此，算术平均值的公式如下：

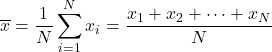
算术平均数也称为算术平均值。

算术平均可能是统计学中最常用的平均类型。

要查看如何获得此类平均值的示例，我们将计算以下数据的算术平均值：

要计算算术平均值，只需将所有统计数据相加，然后除以数据总数，即 6：

加权平均

计算加权平均值时，必须首先将每个统计数据乘以其权重（或权重），然后将所有乘积相加，最后将加权总和除以所有权重之和。

因此，加权平均公式如下：

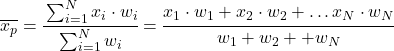
其中 x _i为统计值，w _i为对应的权重。

加权平均值更难以理解，因此我们建议查看以下示例，它逐步解释了它的计算方式：

几何平均值

一组统计数据的几何平均值等于所有值乘积的n次方根。

这种类型的平均值在商业财务中用于计算回报率、平均百分比和复利。

这种存储类型的公式相当复杂。事实上，所有统计集的几何平均值都无法计算，但有时这种类型的平均值无法确定。这就是为什么我们建议您查阅以下链接中解释的所有例外情况：

均方根

均方根等于数据平方算术平均值的平方根。

因此，均方公式如下：

这种类型的平均值也称为均方根、均方根或RMS 。

我们只是指出，三次平均也存在，但它用于非常特殊的情况。

平方平均有优点也有缺点，例如，当统计变量取正值和负值时特别有用，因为通过对每条数据进行平方，所有值都变成正值。您可以通过单击以下链接查看此媒体类型的更多功能：

和谐意义

调和平均值是通过将统计数据总数除以每个值的倒数之和来计算的。

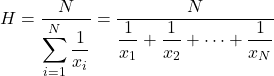
调和平均值用于计算平均速度、时间或进行电子计算。这一特征将调和平均值与其他类型的平均值区分开来，后者经常用于计算价格平均值或百分比。

您可以在下页查看计算此类平均值的示例：

其他类型的丝袜

在本节中，我们将看到其他类型丝袜的公式。我们不会详细介绍每种类型，因为它们的使用并不广泛，但了解还有其他类型的丝袜对您很有好处。

广义平均值是上面看到的平均值类型的混合，并使用以下公式计算：

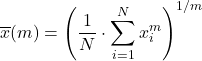
设 f 是单调单射函数，则广义 f 均值定义为：

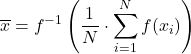
截尾平均值涉及减去样本上端和下端观察值的百分比后计算算术平均值。两端应拒绝相同的百分比。

计算四分位数平均值（也称为四分位数平均值）时，首先丢弃第一和第四四分位数的数据，然后仅计算样本的第二和第三四分位数的算术平均值。因此，此类平均值的公式为：

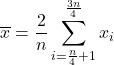
最后，您还可以求出函数的均值。使用以下公式计算闭区间 [a,b] 上的连续函数的平均值：

样本和总体平均值

最后，我们将看看样本平均值和总体平均值之间有什么区别，这两种平均值经常被混淆。

样本均值是对统计样本的值计算的平均值，也就是说，它是对变量的所有值的一部分计算的。

总体平均值是对统计总体（即变量的所有值）计算的平均值。因此，总体平均值与变量的数学期望一致。

如果已知足够大量的数据，则可以认为样本平均值实际上等于总体平均值。但总体平均值的值很难获得，因为实际上分布的所有值很少为人所知。