如何解释曲线残差图(举例)
残差图用于评估回归模型的残差是否呈正态分布以及它们是否表现出异方差性。
理想情况下,您希望残差图中的点随机分散在零值周围,没有清晰的模式。
如果您遇到残差图,其中图点具有曲线图案,则可能意味着您为数据指定的回归模型不正确。
在大多数情况下,这意味着您尝试将线性回归模型拟合到遵循二次趋势的数据集。
以下示例展示了如何在实践中解释(并纠正)曲线残差图。
示例:解释曲线残差图
假设我们收集办公室 11 名不同人员每周工作时数和报告的幸福程度(范围为 0 到 100)的以下数据:

如果我们创建一个简单的工作时间与幸福水平的散点图,它会是这样的:
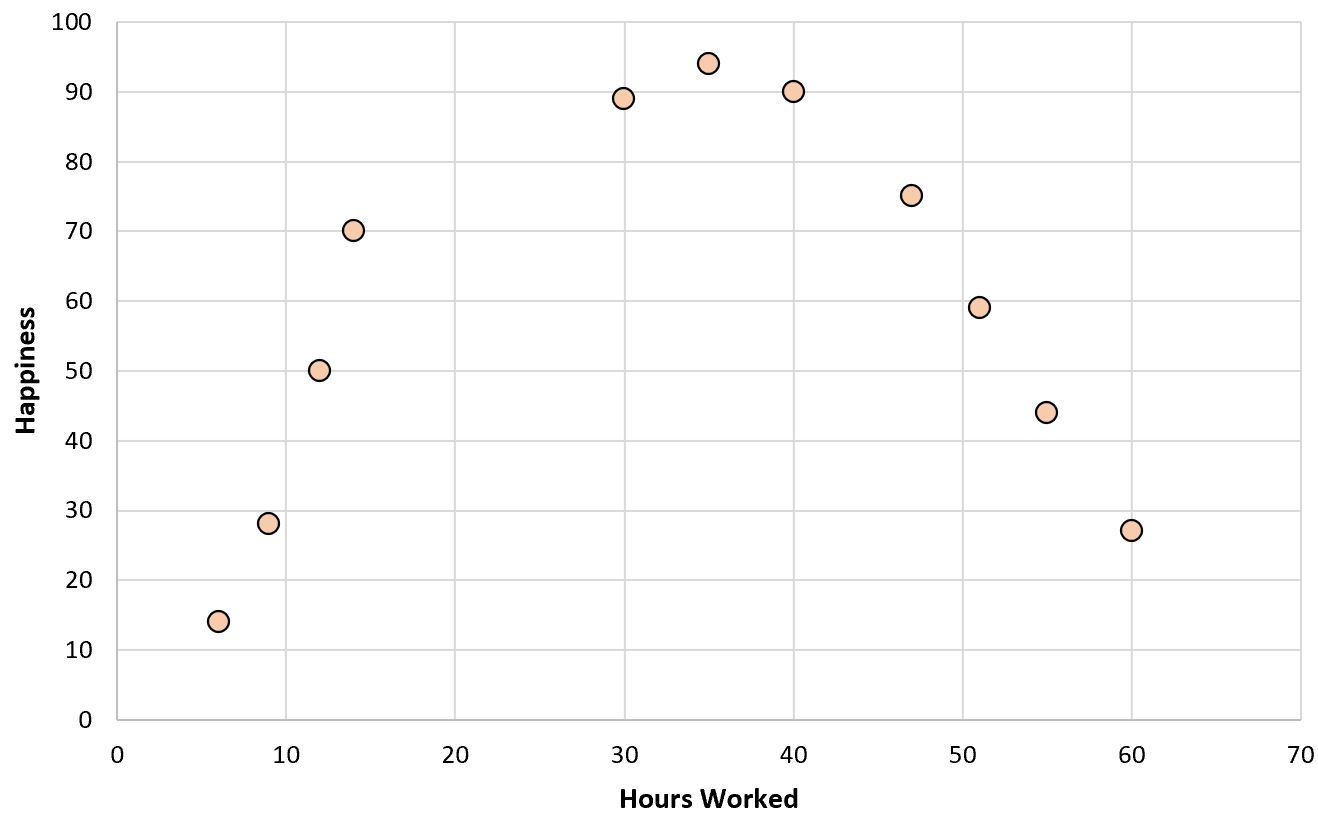
现在假设我们想要使用工作时间来拟合回归模型来预测幸福水平。
以下代码展示了如何将简单的线性回归模型拟合到该数据集并在 R 中生成残差图:
#create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)
#get list of residuals
res <- resid(linear_model)
#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')
#add a horizontal line at 0
abline(0,0)
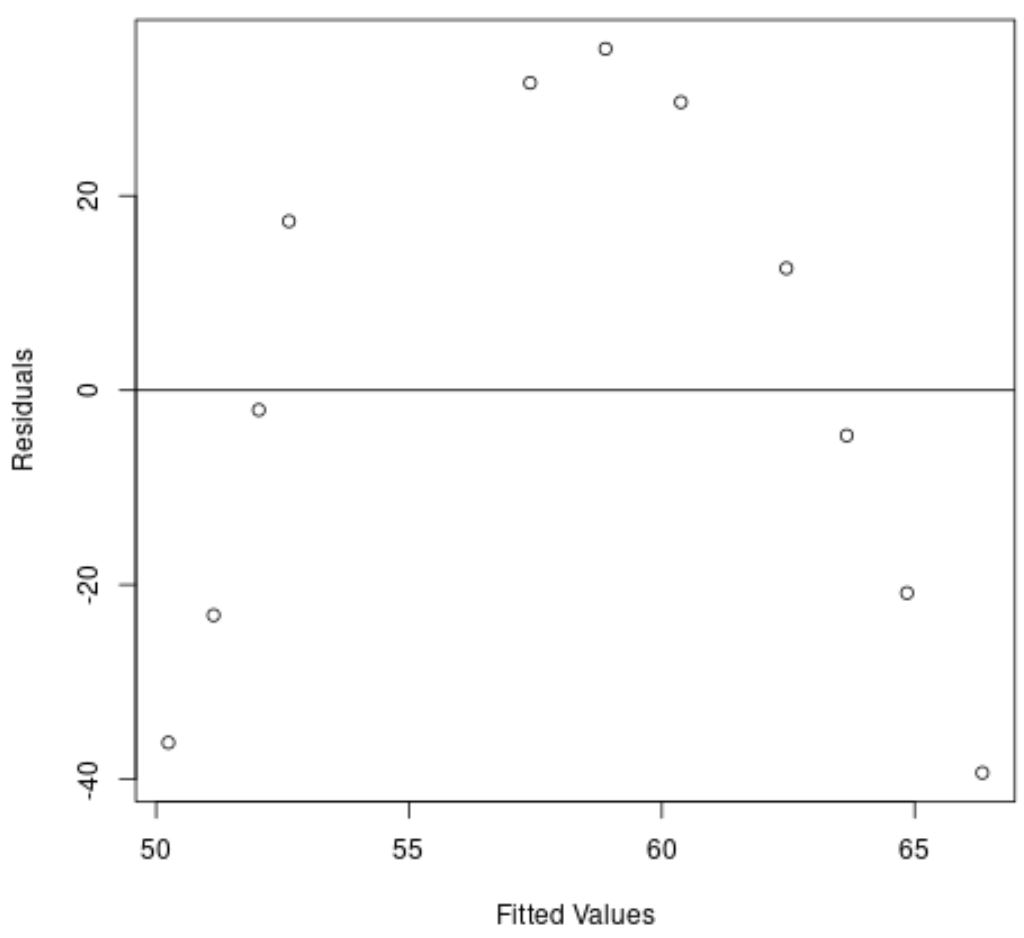
x 轴显示拟合值,y 轴显示残差。
从图中,我们可以看到残差中存在曲线模式,表明线性回归模型无法对该数据集提供合适的拟合。
以下代码展示了如何将二次回归模型拟合到该数据集并在 R 中生成残差图:
#create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2
#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)
#get list of residuals
res <- resid(quadratic_model)
#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')
#add a horizontal line at 0
abline(0,0)
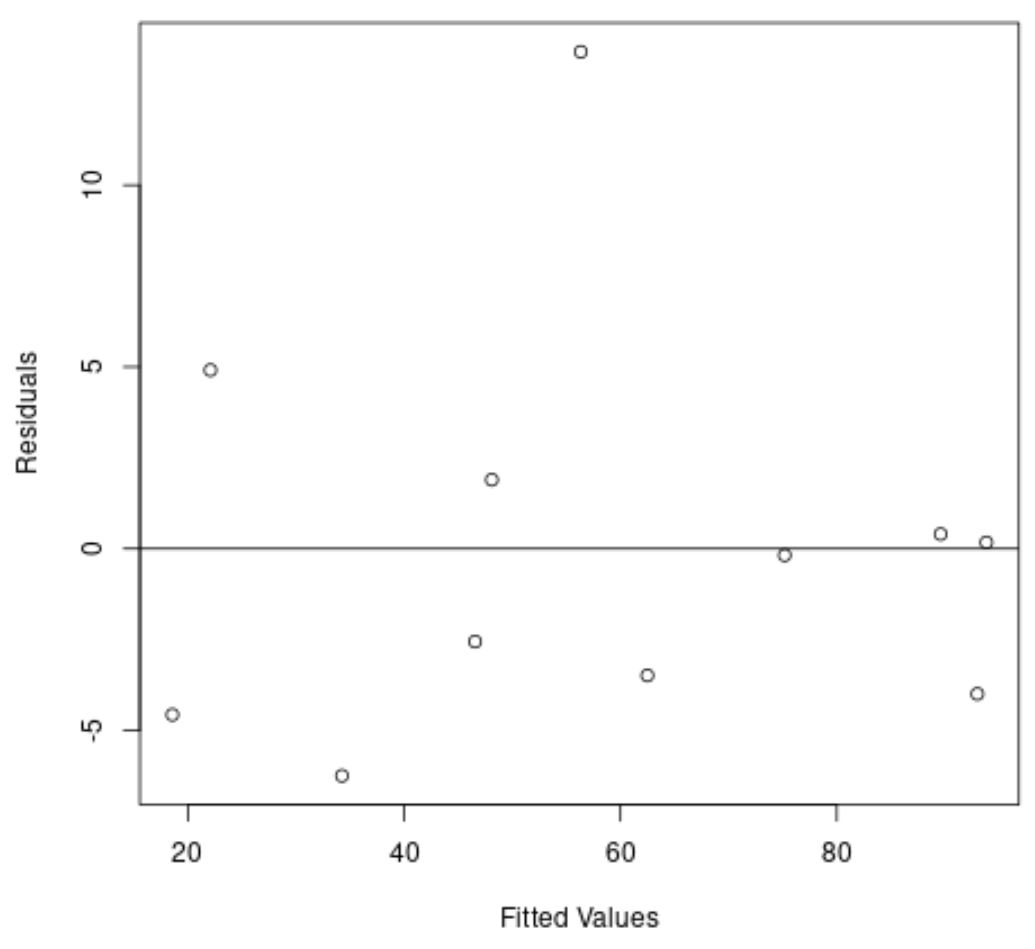
再次,x 轴显示拟合值,y 轴显示残差。
从图中我们可以看到残差随机分散在零附近,并且残差没有明显的趋势。
这告诉我们,二次回归模型比线性回归模型在拟合该数据集方面做得更好。
鉴于我们看到工作时间和幸福水平之间的真正关系似乎是二次方而不是线性关系,这应该是有道理的。
其他资源
以下教程解释了如何使用不同的统计软件创建残差图: