什么是拉丁超立方采样？

拉丁超立方采样是一种可用于对样本均匀分布在样本空间上的随机数进行采样的方法。

它广泛用于生成称为受控随机样本的样本，并且经常应用于蒙特卡罗分析，因为它可以显着减少获得准确结果所需的模拟次数。

样品介绍

要理解拉丁超立方采样的思想，请考虑以下简单示例：

假设我们想从均值为0、标准差为1的正态分布数据集中获取2个值的样本。

如果我们使用真随机数生成器来获取这个样本，有可能两个值都大于0，或者两个值都小于0。

但是，如果我们使用拉丁超立方采样来获取这个样本，那么就可以保证一个值大于0，另一个值小于0，因为我们可以将样本空间专门划分为值大于0的区域和一个值小于0的区域，然后从每个区域中选择一个随机样本。

一维拉丁超立方采样

一维拉丁超立方采样背后的想法很简单：将给定的CDF划分为n 个不同的区域，并在每个区域中随机选择一个值以获得大小为n的样本。

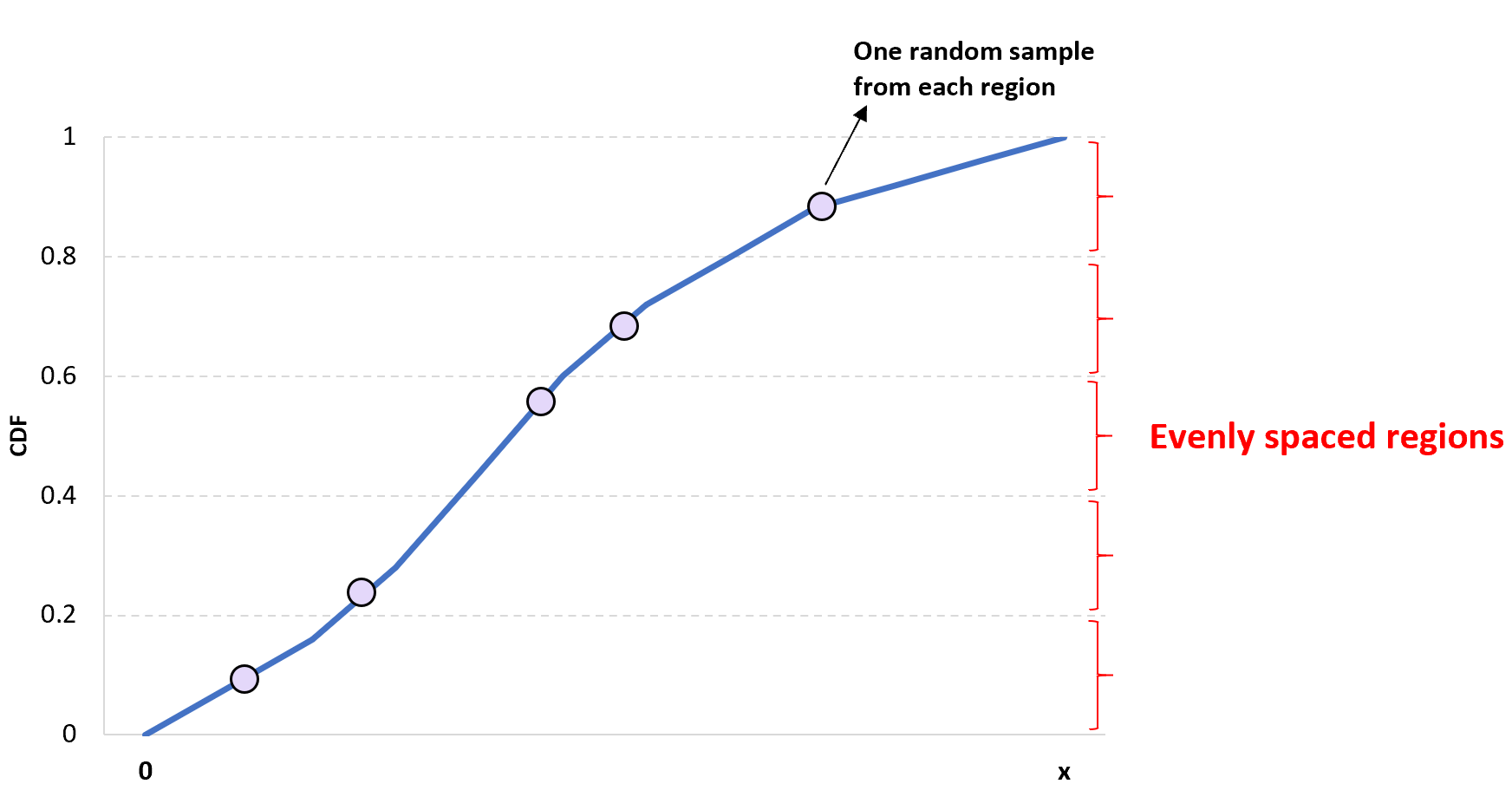
这种方法的优点是它确保样本中至少包含每个区域的一个值。

二维拉丁超立方体采样

我们也可以轻松地将一维拉丁超立方采样的思想扩展到二维。

对于x和y两个变量，我们可以将每个变量的样本空间划分为n个均匀分布的区域，并从每个样本空间中选择一个随机样本，从而获得二维上的随机值。

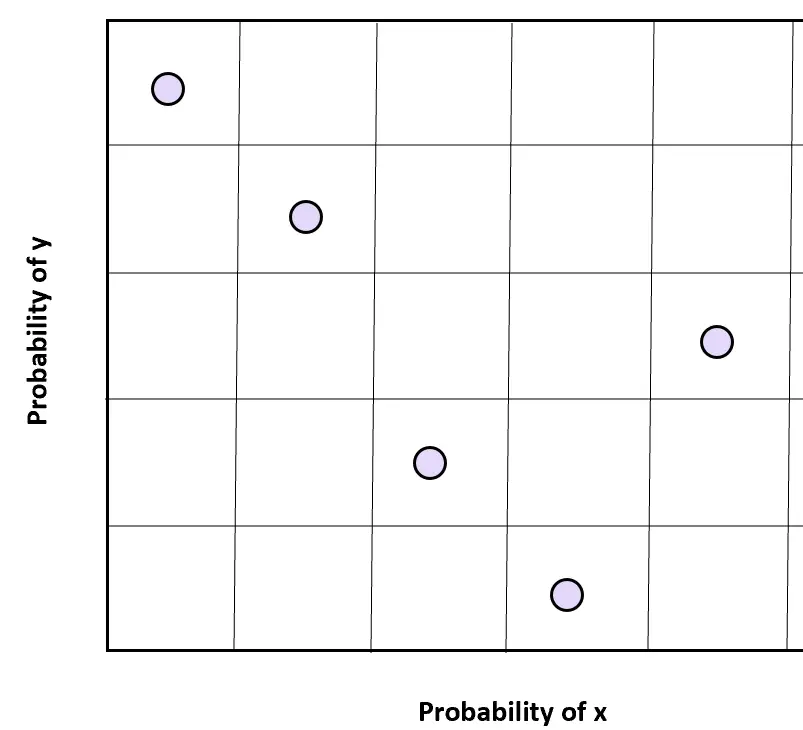
值得注意的是，对于这种采样技术来说，两个变量必须是独立的，才能达到预期的结果。

N 维拉丁超立方采样

为了在更大的维度上执行拉丁超立方采样，我们可以简单地将二维拉丁超立方采样的思想扩展到更多维度。

每个变量被简单地划分为均匀间隔的区域，然后从每个区域中选择随机样本以获得受控随机样本。

相关：什么是高维数据？

为什么使用拉丁超立方采样？

拉丁超立方采样的主要优点是它生成的样本反映了真实的基础分布，并且往往需要比简单随机采样小得多的样本量。

如果您正在处理具有大量维度的数据并且需要获取确保反映数据的真实基础分布的随机样本，则这种采样方法可能特别有用。