什么是斯坦宁分数？ （定义和示例）

Stanine 分数是“标准九分”的缩写，是一种按标准九分制衡量测试分数的方法。

使用这种方法，我们可以将每个测试结果从原始分数（即0到100）转换为1到9之间的数字。

我们使用一个简单的两步过程来使测试结果适应 Stanine 分数：

1.将每个测试结果从最低到最高排序。

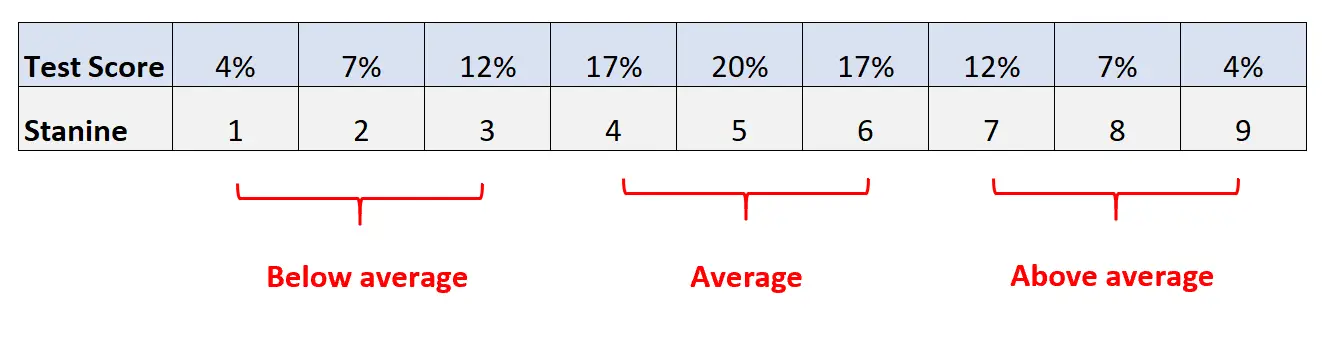
2.根据下表，将最低 4% 的分数赋予 stanine 分数，将次低的 7% 分数赋予 stanine 分数 2，依此类推：

一般来说，我们考虑测试结果如下：

• 斯坦尼斯 1、2、3：低于平均水平
• 斯坦尼斯 4、5、6：平均
• 斯坦尼斯 7、8、9：高于平均水平

事实证明，Stanine 量表的平均值为 5，标准差为 2。

Stanine 分数的优点和缺点

Staniine 分数具有以下优点和缺点：

好处： Stanine 分数使我们能够快速了解给定的测试分数与所有其他测试结果的关系。

例如，我们知道一个 stanine 5 考试成绩的学生在所有考试成绩中处于中间 20%。我们知道，一名落入stanine 9的学生的考试成绩在所有成绩中排名前4%。

缺点：使用斯坦尼斯的缺点是每个斯坦尼斯的大小不同，并且给定斯坦尼斯的测试分数与其自身斯坦尼斯的分数相比可能更接近下一个斯坦尼斯的分数。

例如，得分在 40% 和 60% 之间的学生都被分为 5 级。但是，测试成绩在 58% 之间的学生将比大多数分数更接近 6 级的分数。在斯坦尼 5 收到。

斯坦宁分数替代方案

stanine 分数的两种替代方法是百分位数和 z 分数。

1.百分位数告诉我们给定测试分数高于该分数的所有分数的百分比。

例如，第 90 个百分位数的分数高于所有测试分数的 90%。位于第 50 个百分位数的测试分数恰好位于所有测试分数的中间。

2. z 分数告诉我们给定分数与平均值的标准差有多少。计算方法如下：

z = (X – μ) / σ

金子：

• X 是单个原始数据值
• μ 是数据集的平均值
• σ 是数据集的标准差

我们对 z 分数的解释如下：

• z 分数为正表示测试分数高于平均水平
• z 分数为负表示测试分数低于平均水平
• z 分数为零表示测试分数完全等于平均值

z 分数距离零越远，给定的测试分数距离平均值就越远。

Z 分数和百分位数让我们更准确地了解某些测试分数与 Stanine 分数相比的排名情况。