如何在 google 表格中计算 spearman 排名相关性

在统计学中，相关性是指两个变量之间关系的强度和方向。相关系数的值范围为 -1 到 1，具有以下解释：

• -1：两个变量之间完美的负关系
• 0：两个变量之间没有关系
• 1：两个变量之间完美的正相关关系

一种特殊类型的相关性称为Spearman 等级相关性，用于衡量两个排名变量之间的相关性。 （例如，学生的数学考试成绩相对于其在班级中的科学考试成绩的排名）。

本教程介绍如何计算 Google 表格中两个变量之间的斯皮尔曼等级相关性。

示例：Google 表格中的 Spearman 等级相关性

执行以下步骤来计算特定班级 10 名学生的数学考试成绩和科学考试成绩之间的 Spearman 等级相关性。

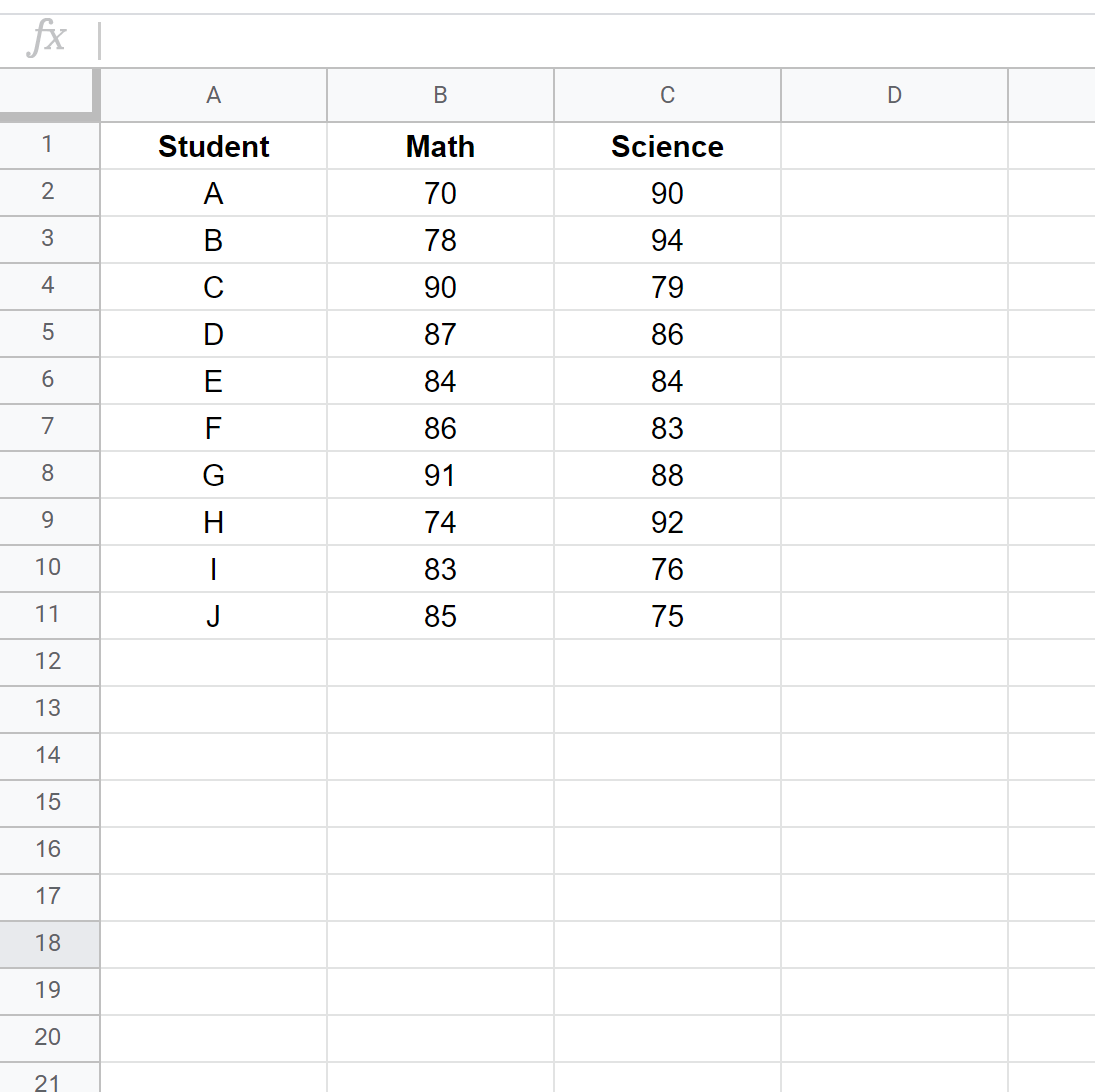
第 1 步：输入数据。

在两个单独的列中输入每个学生的考试结果：

步骤2：计算每项考试成绩的排名。

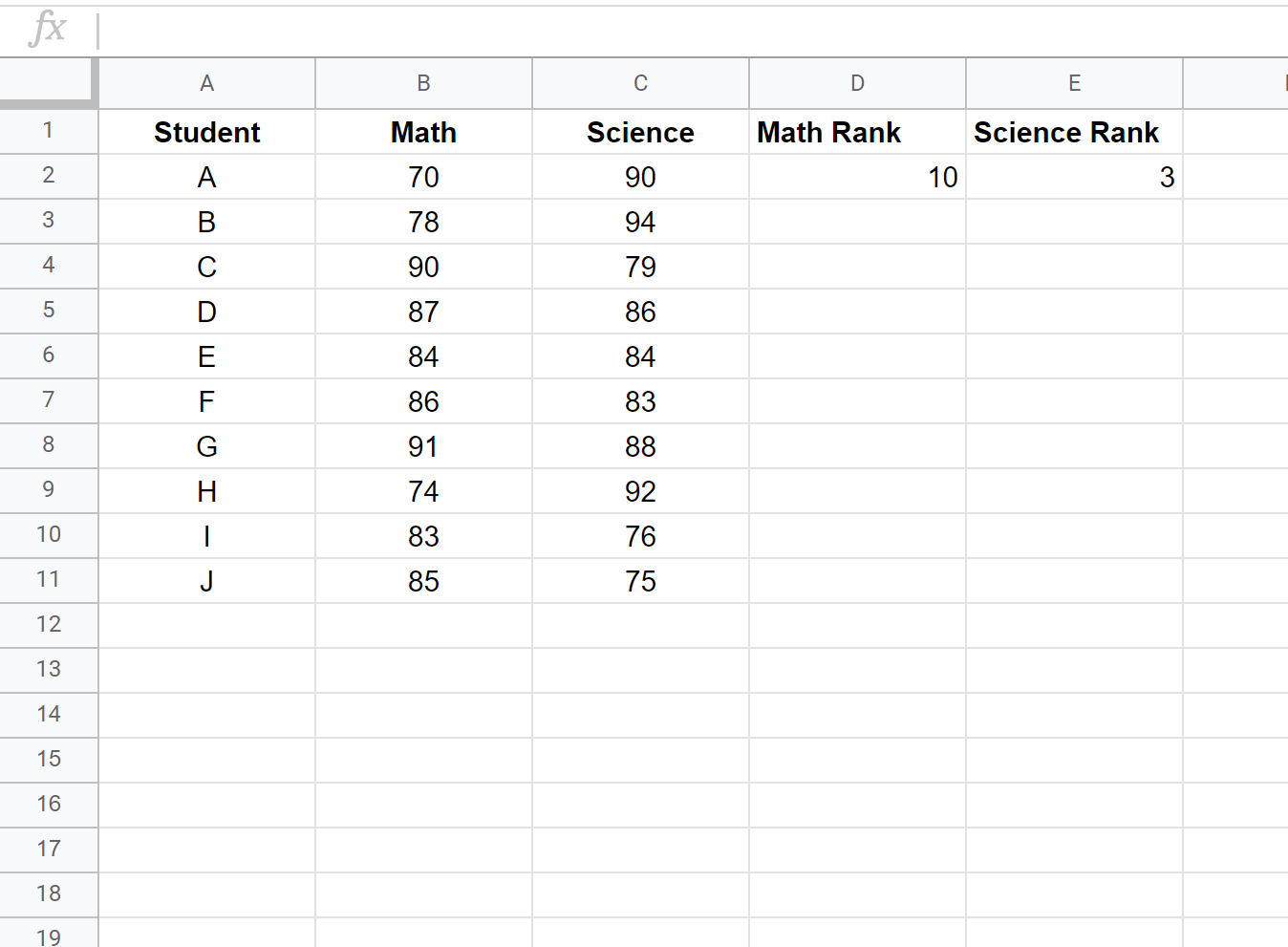
接下来，我们将计算每项考试成绩的排名。在单元格 D2 和 E2 中使用以下公式计算第一个学生的数学和科学排名：

单元格 D2： =RANK.AVG(B2, $B$2:$B$11, 0)

单元格 E2： =RANK.AVG(C2, $C$2:$C$11, 0)

接下来，突出显示要填充的剩余单元格：

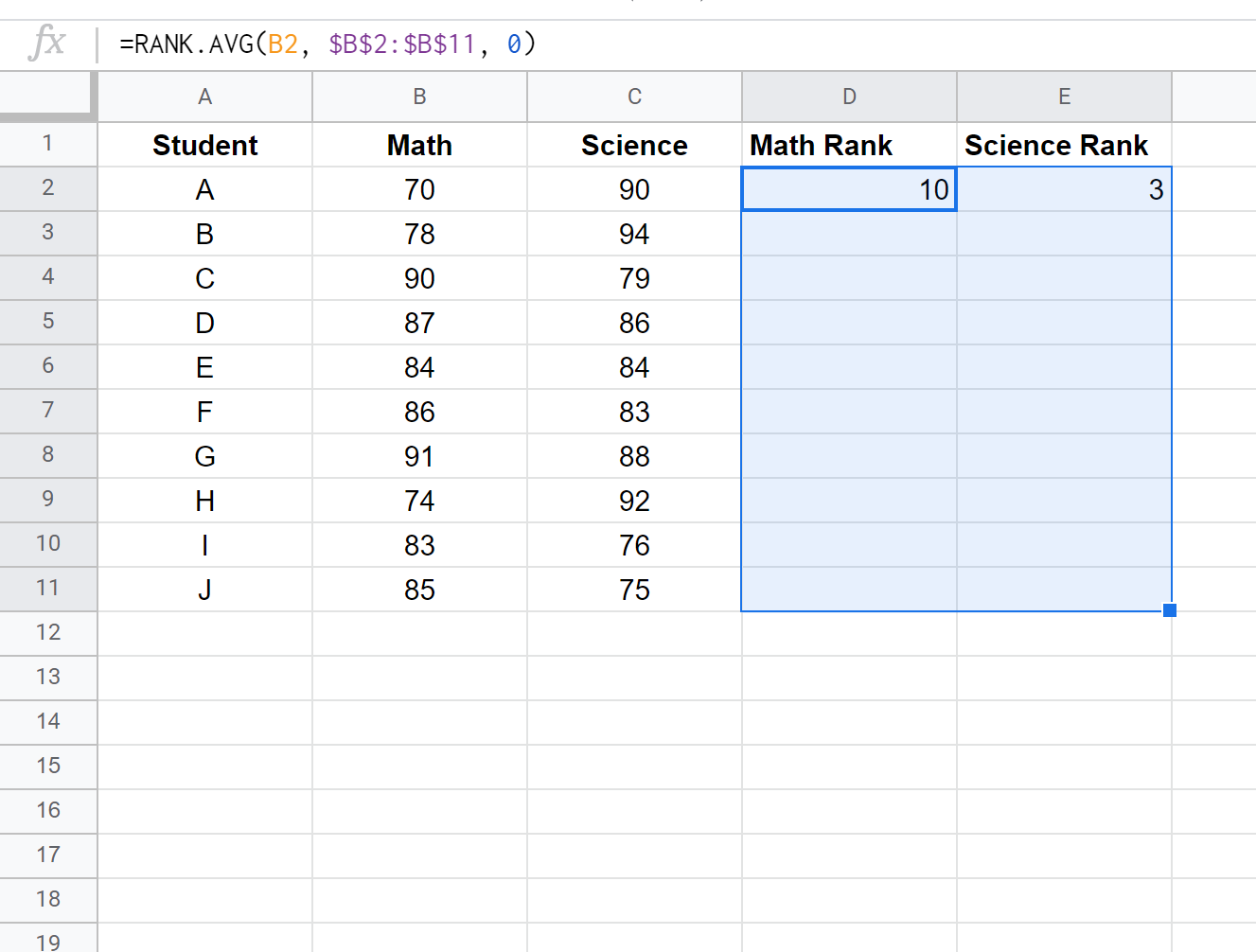
然后点击Ctrl+D即可进入每个学生的排名：

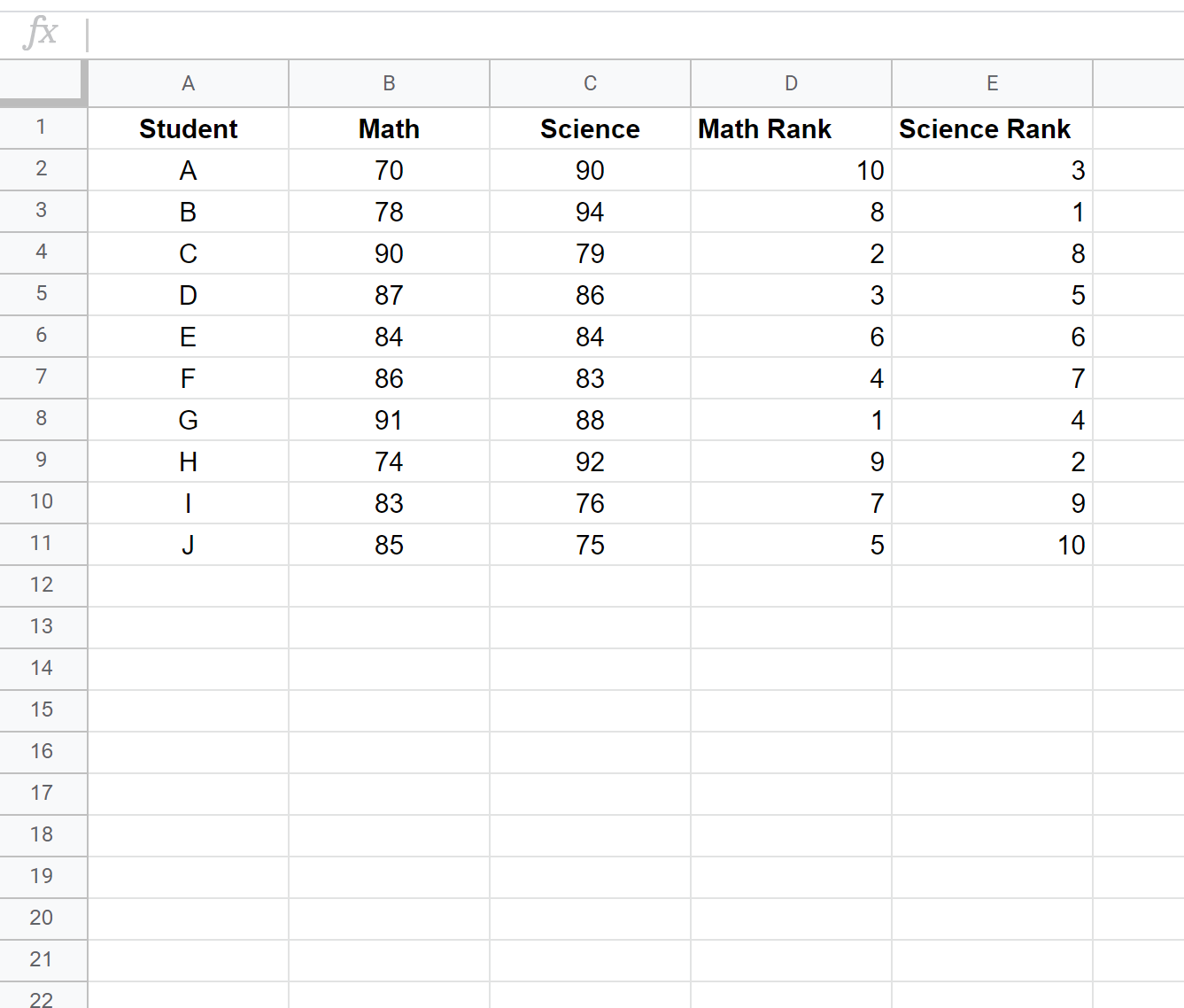
步骤3：计算Spearman等级相关系数。

最后，我们将使用CORREL()函数计算数学分数和科学分数之间的斯皮尔曼等级相关系数：

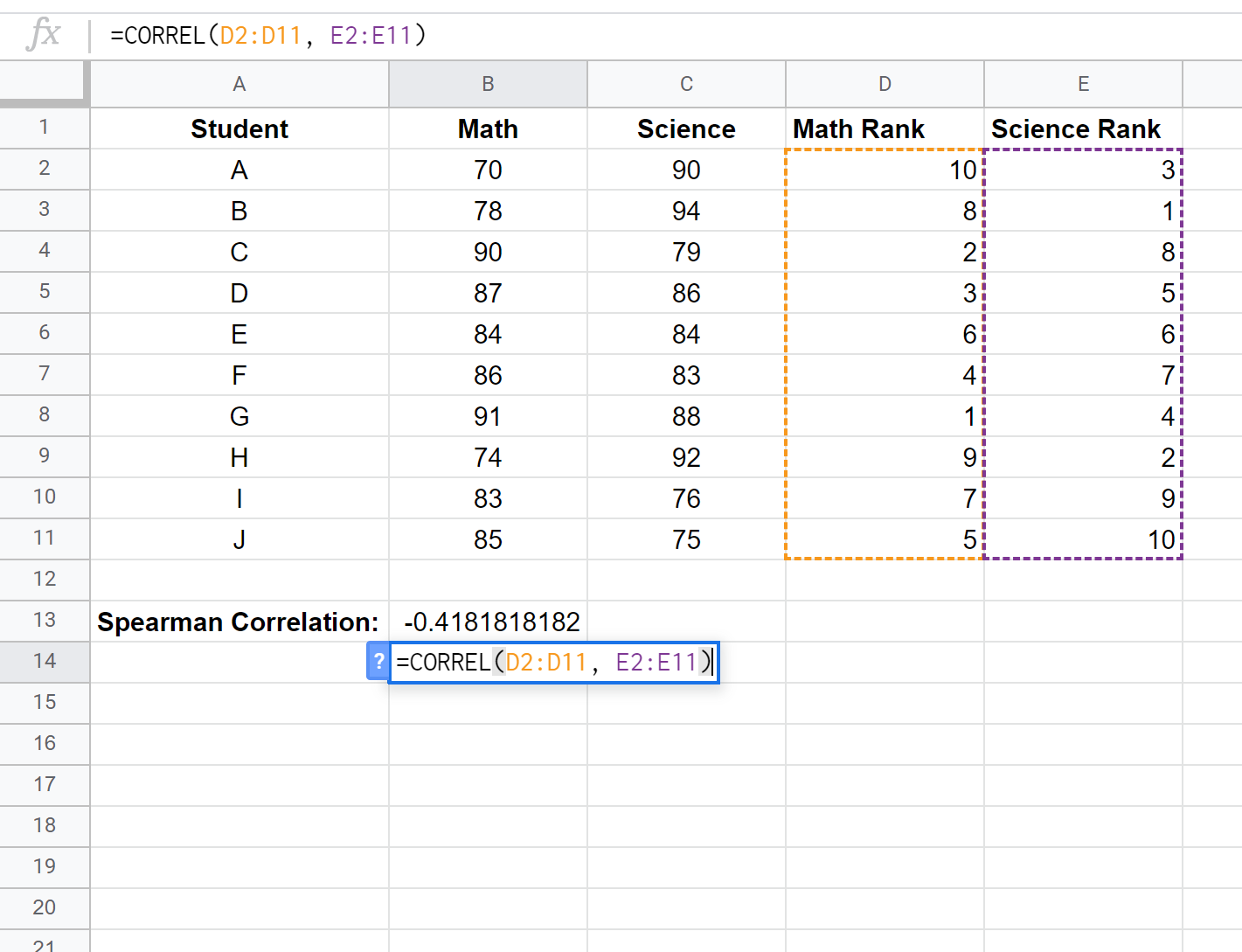
Spearman 等级相关性结果为-0.41818 。

步骤 4（可选）：确定 Spearman 等级相关性是否具有统计显着性。

在上一步中，我们发现数学和科学考试成绩之间的斯皮尔曼等级相关性为-0.41818 ，表明两个变量之间呈负相关。

然而，为了确定这种相关性是否具有统计显着性，我们需要参考临界值的斯皮尔曼等级相关表，该表显示了与不同样本量（n）和显着性水平（α）相关的临界值。

如果我们的相关系数的绝对值大于表中的临界值，则两个变量之间的相关性具有统计显着性。

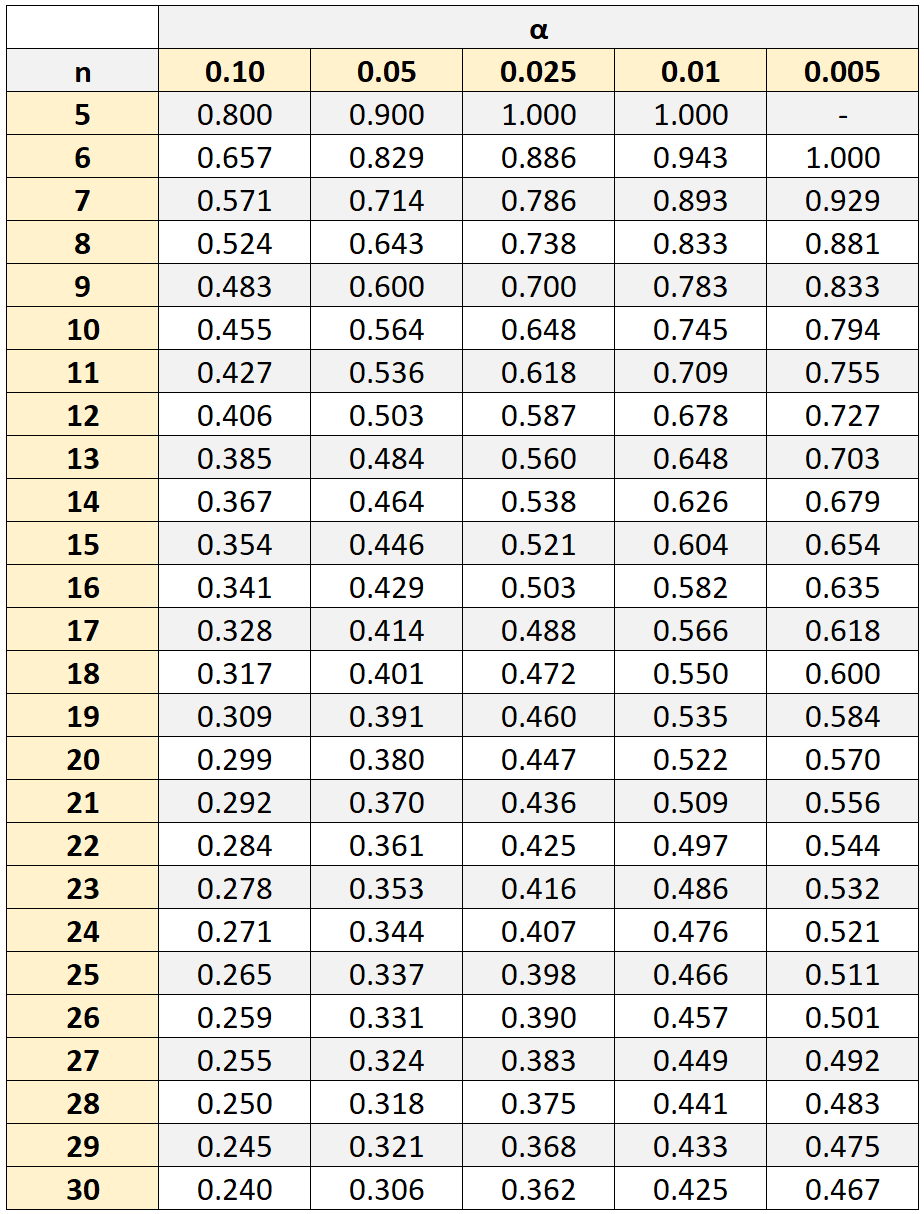
在我们的示例中，样本量为 n = 10 名学生。使用 0.05 的显着性水平，我们发现临界值为0.564 。

由于我们计算的斯皮尔曼等级相关系数的绝对值（ 0.41818 ）不大于这个临界值，这意味着数学和科学分数之间的相关性在统计上不显着。

相关： 如何在 Excel 中计算斯皮尔曼等级相关性