方差

经过 1月 25, 2023 统计数据 ％ 评论

在本文中，我们将解释什么是方差（也称为均方偏差）以及它的计算方法。您将找到方差公式，方差计算的具体示例，此外，您将能够使用在线计算器计算任何数据集的方差。

我们还向您展示如何查找分组数据的方差，因为这是通过不同的方式完成的。最后，我们教您总体方差和样本方差之间的差异、方差和标准差之间的差异以及该统计度量的属性。

什么是方差？

在统计学中，方差是离散度的度量，表明随机变量的变异性。方差等于残差平方和除以观测值总数。

请记住，残差被理解为统计数据点的值与数据集平均值之间的差。

在概率论中，方差的符号是希腊字母 sigma squared (σ 2 )。尽管它通常也表示为Var(X) ，其中 X是计算方差的随机变量。

一般来说，解释随机变量的方差值很简单。方差值越大，数据越分散。反之亦然，方差值越小，数据序列中的离散性就越小。然而，在解释方差时，必须小心异常值，因为它们可能会扭曲方差值。

方差，除了离差之外，其他被认为是方差的度量还有极差、标准差、平均差和变异系数。

如何计算间隙

要计算方差，必须执行以下步骤：

  1. 求数据集的算术平均值。
  2. 计算残差，定义为数据集的值与平均值之间的差。
  3. 对每个余数进行平方。
  4. 将上一步计算出的所有结果相加。
  5. 除以数据总数。得到的结果就是数据序列的方差。

综上所述，数据集方差的计算公式为：

方差

金子：

  • X 是要计算方差的随机变量。
  • x_i 是数据值
  • n 是观测值的总数。
  • \overline{X} 是随机变量的平均值
  • X 是方差或均方偏差

👉您可以使用下面的计算器来计算任何数据集的方差。

因此，要从数据系列中提取方差，了解算术平均值的计算方式至关重要。如果您不记得如何执行此操作，可以在上面链接的文章中查看。

偏差示例

现在我们知道了方差的定义，我们将逐步解决一个练习，以便您了解如何获得数据序列的方差。

  • 对于一家跨国公司来说，过去五年的经济成果是众所周知的，大部分都获得了利润，但有一年却出现了相当大的损失：11.5, 2, -9, 700 万欧元。计算该数据集的方差。

正如我们在上面的解释中看到的，要找到数据序列的方差，我们需要做的第一件事是计算其算术平均值：

\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2

一旦我们知道了数据的平均值，我们就可以使用方差公式：

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}

我们将练习报表提供的数据代入公式：

Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}

最后，剩下的就是解决计算方差的运算：

\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}

请注意，方差单位与统计数据的单位相同，但进行了平方，因此该数据组的方差为 4576 万欧元2 。

差距计算器

在以下计算器中输入统计数据集以计算其方差。数据必须用空格分隔，并使用句点作为小数点分隔符输入。

分组数据的方差

要计算分组为区间 的数据的方差，必须遵循以下步骤：

  1. 求分组数据的平均值。
  2. 计算分组数据的残差。
  3. 对每个余数进行平方。
  4. 将之前的每个结果乘以其间隔的频率。
  5. 将上一步获得的所有值相加。
  6. 除以观察总数。所得数字是分组数据的方差。

换句话说，分组数据的方差计算公式如下：

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}

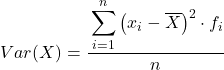
尽管通常使用上面的公式，但也可以使用下面的代数表达式，因为它是等效的：

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2

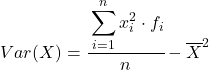
例如，我们将找到以下分组数据系列的方差：

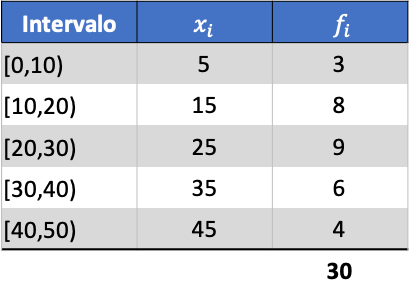
数据按区间分组

首先，我们需要确定分组数据的平均值。为此，我们在频率表中添加一列，其中包含类别标记和频率的乘积：

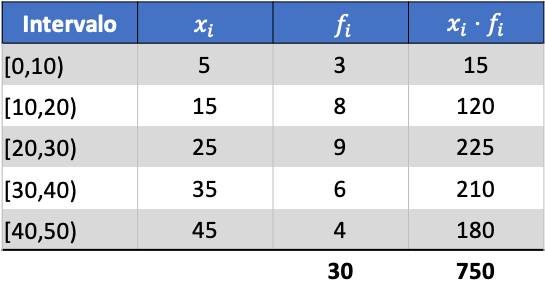
数据按平均值分组

现在，我们通过将添加列的总和除以数据总数来计算分组数据的平均值：

\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25

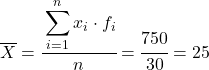
根据计算数据的平均值，我们可以添加以下三列：

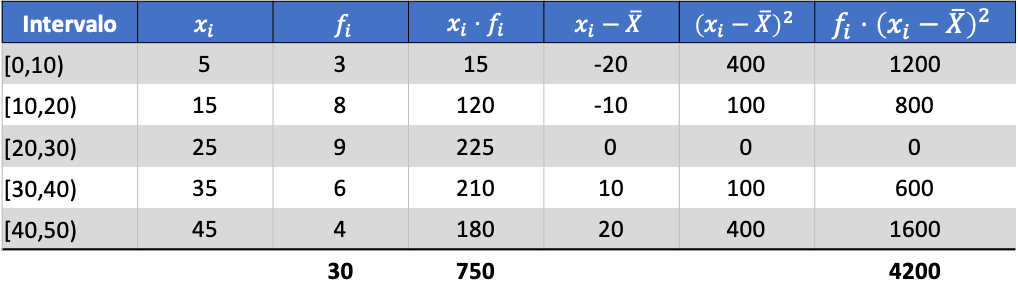
分组数据的方差

因此，合并数据集的方差是最后一列的总和除以观察数据的总数：

Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140

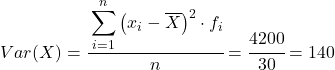
方差和标准差

方差和标准差（或标准差）是离散度的两种度量，因此都表示数据集的离散程度。然而，方差和标准差之间的区别在于，方差通常具有较大的值，因为它是标准差的平方。

标准差通常由希腊字母 sigma (σ) 表示，因此方差由字母 sigma square (σ 2 ) 表示，因为它是这两个离散度量之间存在的数学关系。

Var(X)=\sigma^2

因此，一旦计算了一组数据的方差值，只需取方差的平方根，您就可以轻松找到同一组数据的标准差值。

\sigma=\sqrt{\sigma^2}

总体方差和样本方差

从逻辑上讲，总体方差是指统计总体方差的计算，而样本方差是指样本方差的计算。然而，这是两个不同的概念，因为总体方差公式与样本方差公式不同。

通常在方差练习中，如果他们没有另外告诉我们，要找到所提供数据集的方差，我们必须使用总体方差公式，这是我们在文章开头解释的公式：

\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}

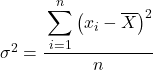
但也许在某些问题中你会被要求将统计数据视为样本，在这种情况下我们需要使用样本方差公式：

s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}

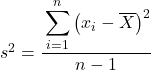
请注意，为了表示正在计算总体方差，用希腊字母 σ 表示，但在计算样本方差时则使用字母 s。

正如你所看到的，两个公式之间的唯一区别是，在样本的方差中，我们需要除以观察总数负1，例如，如果总共有30个数据项，我们将除以29但分子的计算是以完全相同的方式完成的。

方差属性

方差具有以下属性：

  • 任何随机变量的方差将始终大于或等于零。同样，如果方差为零，则意味着所有统计数据都是相同的。

Var(x)\ge 0

  • 显然，单个值的方差为零。

Var(a)=0\qquad a\in \mathbb{R}

  • 标量与变量的乘积的方差等于该标量的平方乘以变量的方差。

Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}

  • 两个因变量之和的方差等于每个变量各自的方差之和加上两个变量之间协方差的两倍。

Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)

  • 因此，如果两个变量是独立的，为了确定它们总和的方差，将它们的方差相加就足够了：

Var(X+Y)=Var(X)+Var(Y)

  • 偏差也可以使用以下公式通过数学期望来定义：

Var(X)=E\bigl[(X-\overline{X})^2\bigr]

关于作者

安德森博
本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多

％ 评论

  1. 杨菲菲

    开头第一句“在本文中，我们解释什么是方差，也称为方差”，是不是有误啊

    回复

添加评论

您的电子邮箱地址不会被公开。 必填项已用*标注