本福德定律
本文解释什么是本福德定律。此外,您将能够了解本福德定律是如何被发现的以及该统计定律的应用。
什么是本福德定律?
本福德定律,也称为第一位数字定律,是一种统计定律,表示一段数据的第一位数字为 1 的概率大于它为另一个数字的概率。
换句话说,本福德定律说的是,在现实生活中存在的一组数值数据中,数字1是作为数据第一位重复次数最多的数字。
此外,数字越高,最终获得第一名的可能性就越小。因此,第一个数字更有可能是 1,而不是 2,但 2 比 3 更有可能,3 比 4 更有可能,依此类推。
本福德定律得名于美国人弗兰克·本福德。尽管本福德不是他发明的,但他普及了这一统计规则。下面我们就来看看本福德定律的由来。
本福德定律公式
本福德定律指出,第一个数字是某个数字的概率等于该数字的一加一的对数。
因此,本福德定律的公式如下:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a77defb5b209293a074ac2bee02c2e07_l3.png)
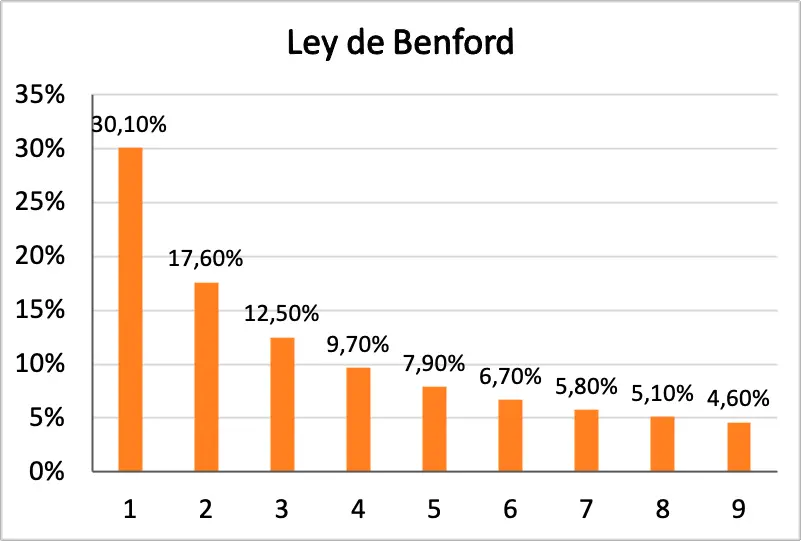
因此,从本福德定律公式中,我们可以推导出每个数字是数据项第一位数字的概率。在下表中您可以看到所有概率的百分比:
| 数字 | 概率 是第一个数字 |
|---|---|
| 1 | 30.1% |
| 2 | 17.6% |
| 3 | 12.5% |
| 4 | 9.7% |
| 5 | 7.9% |
| 6 | 6.7% |
| 7 | 5.8% |
| 8 | 5.1% |
| 9 | 4.6% |
此外,您可以在下面看到一个直方图,其中以图形方式表示了本福德定律的所有概率:
本福德定律的历史
1881 年,数学家西蒙·纽科姆 (Simon Newcomb) 发现对数表的第一页比最后一页的使用次数要多得多,由此推导出了本福德定律。这意味着数字的前几个数字出现的可能性并不相同,但 1 比 2 出现的频率更高,2 比 3 出现的频率更高,依此类推,直到 9。
然而,纽科姆没有留下任何统计证据来表明这条规则被遵循,他只是根据对数表的磨损进行了推演。
后来,特别是在 1938 年,物理学家弗兰克·本福德(Frank Benford)也做出了同样的观察,并做了一个实验来实证验证。在来自20个不同样本的20,229个值的统计数据集上,他对每个数据的第一位数字进行了研究。因此,根据结果,他证明了本福德定律的满足,并推导出了一个公式,使他能够计算出第一个数字是某个数字的概率(我们在上面看到了这个公式)。
简而言之,虽然本福德定律是由西蒙·纽科姆(Simon Newcomb)首先发现的,但他以弗兰克·本福德(Frank Benford)的名字命名,因为他是验证这一统计定律的人。
本福德定律的应用
本福德定律是一种统计定律,可应用于非常不同的领域。例如,本福德定律广泛应用于经济学、生物学,甚至政治学。
在经济学中,本福德定律经常被用来检测数据操纵,因为如果一个数据集不符合本福德定律,就表明该数据被操纵了。例如,该法律用于侦查可能的税务欺诈案件。
应该注意的是,本福德定律不用于证明随机现象的真实性,因为结果是等概率的。因此,本福德规则不能用于验证彩票结果。
另一方面,在遗传学中,本福德定律可用于分析不同类型生物之间基因组长度的差异。
最后,还尝试通过应用本福德定律来检测选民欺诈,尽管它在这种情况下的有用性受到质疑。