样本标准差（或样本标准差）

本文解释了统计学中的样本标准差。同样，您将学习如何计算样本标准差、已解决的练习以及样本标准差和总体标准差之间的区别。最后，您可以使用在线计算器计算任何样本标准差。

样本标准差是多少？

样本标准差（或样本标准差）是衡量分散度的指标，表明样本的变异性。更准确地说，样本标准差等于偏差平方和除以样本量减一的平方根。

样本标准差的符号是小写字母s 。

样本标准差有时也称为拟标准差（或准标准差），以区别于总体标准差。下面我们将看到样本标准差与总体标准差有何不同。

标准差公式示例

样本标准差等于样本数据偏差平方和除以样本量减一后的平方根。因此，样本标准差的计算公式为：

金子：

• 

  是样本标准差（或样本标准差）。

• 

  是数据值

  

  。

• 

  是样本大小

• 

  是样本均值。

👉您可以使用下面的计算器来计算任何数据样本的标准差。

计算样本标准差的示例

现在我们知道了样本标准差（或样本标准差）的定义及其公式是什么，我们将解决一个简单的示例来完成对它的计算方式的理解。

• 一家鞋业公司正在进行市场调查，以决定是否推出新鞋款。因为有许多不同的型号，并且您只想进行快速的初步分析，所以您决定只查看前五个竞争鞋品牌的样本价格（价格如下所示）。该数据集的标准差是多少？

€98 €70 €125 €89 €75

为了计算样本标准差，我们首先需要计算样本均值：

计算出样本均值后，我们应用样本标准差公式：

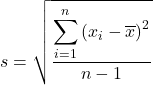
我们将样本数据代入公式：

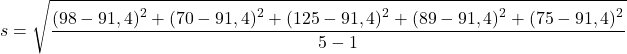
因此，剩下的就是解决计算样本标准差的运算：

因此，分析样本的抽样差异为 21.82 欧元。

样本标准差和总体标准差

接下来，我们将看看样本标准差和总体标准差之间有什么区别，因为这是我们需要明确的两个相关的统计概念。

在estadística中，总体的标准差是用总体的所有元素计算得到的标准差，尽管标准差是仅用总体中的一个数据样本进行计算得到的标准差。

从数学上讲，样本标准差和总体标准差之间的差异是用于计算的公式的分母。要计算样本标准差，必须除以n-1，而总体标准差则要除以n。

此外，为了区分样本标准差和总体标准差，它们用不同的符号表示。样本标准差的符号是字母 s，而总体标准差的符号是希腊字母 σ。

一般来说，并非总体的所有元素都是已知的，因此统计研究是对总体样本进行的。因此，样本标准差用于对整个总体的标准差值进行点估计。

标准差计算器示例

将样本的数据输入以下在线计算器即可计算其样本标准差（或样本标准差）。数据必须用空格分隔，并使用句点作为小数点分隔符输入。