正态分布和标准正态分布：区别

正态分布是统计学中最常用的概率分布。

它具有以下属性：

• 对称
• 钟形
• 平均值和中位数相等；均位于分布的中心

正态分布的均值决定其位置，标准差决定其分布。

例如，下图显示了具有不同均值和标准差的三个正态分布：

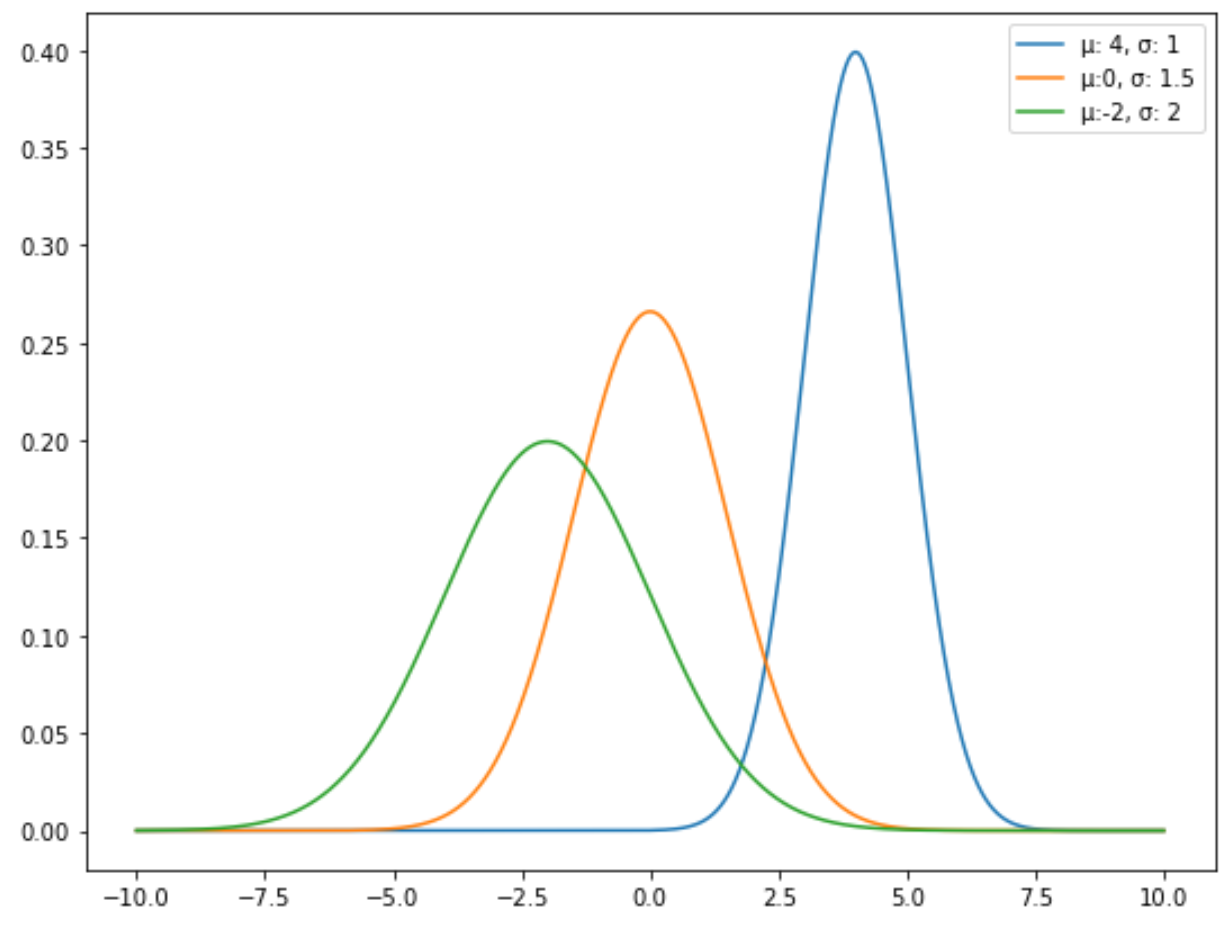
标准正态分布是一种特定类型的正态分布，其平均值为 0，标准差为 1。

下图显示了标准正态分布：

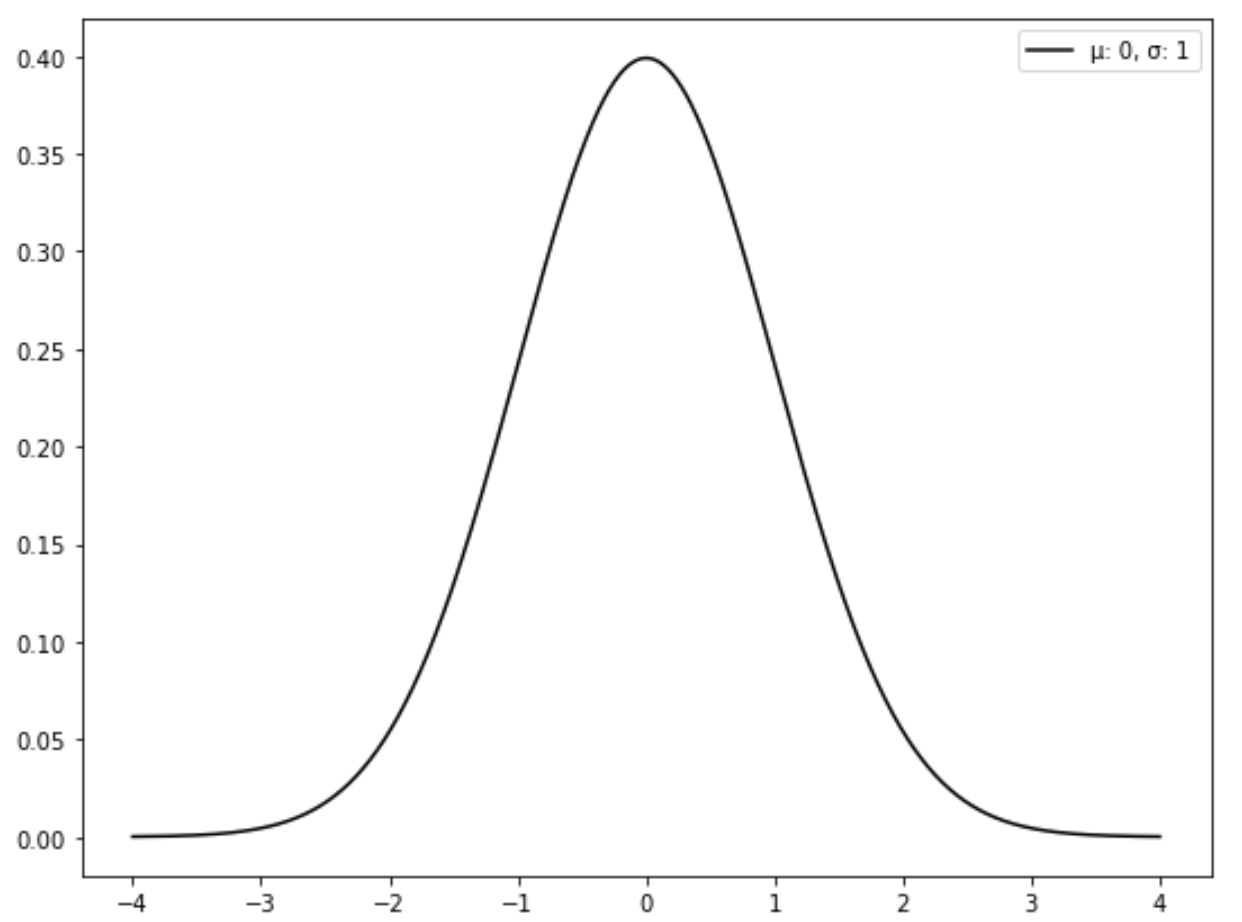
如何将正态分布转换为标准正态分布

任何正态分布都可以通过将数据值转换为 z 分数来转换为标准正态分布，使用以下公式：

z = (x – μ) / σ

金子：

• x：个体数据的值
• μ：分布的平均值
• σ：分布的标准偏差

例如，假设我们有以下数据集，平均值为 6，标准差为 2.152：

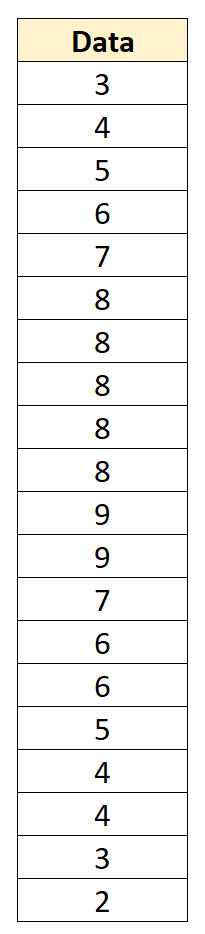
我们可以通过从每个值中减去 6 再除以 2.152，将每个单独的数据值转换为 z 分数：

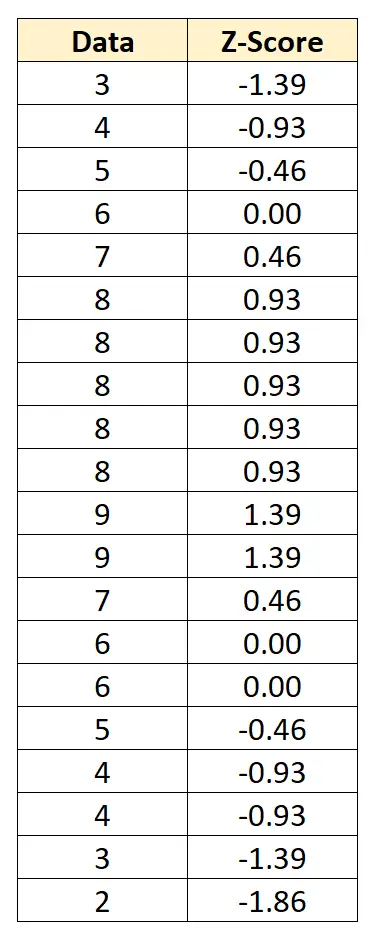
z 分数告诉我们每个数据点与平均值的标准差有多少。例如，第一个数据值“3”比平均值低 1.39 个标准差。

该分数分布的平均值为零，标准差为一。

如何使用标准正态分布

标准正态分布具有以下属性：

• 大约 68% 的数据落在平均值的一个标准差范围内
• 大约 95% 的数据落在平均值的两个标准差之内。
• 大约 99.7% 的数据落在平均值的三个标准差范围内。

这被称为经验法则，用于理解数据集中值的分布。

例如，假设某个花园中植物的高度呈正态分布，平均值为 47.4 英寸，标准差为 2.4 英寸。

根据经验，高度低于 54.6 英寸的植物所占的百分比是多少？

经验法则表明，对于给定的正态分布数据集，99.7% 的数据值落在平均值的三个标准差范围内。这意味着 49.85% 的值落在平均值和高于平均值三个标准差之间。

在此示例中，54.6 比平均值高三个标准差。由于我们知道正态分布中 50% 的数据值小于均值，因此总共 50% + 49.85% = 99.85% 的值小于 54.6。

所以99.85%的植物高度都低于 54.6 英寸。

其他资源

实践经验法则时遇到的问题
经验法则计算器
如何在 Excel 中应用经验法则