比例的置信区间

经过本杰明·安德森博 8月 3, 2023 统计数据 0 条评论

本文解释了比例的置信区间是什么以及它在统计中的用途。同样，您将了解如何计算比例的置信区间以及已解决的练习，以更好地理解该概念。

该比例的置信区间是多少？

比例的置信区间是为总体比例提供可接受值范围的区间。即，比例的置信区间表示人口比例处于其间且具有误差范围的最大值和最小值。

例如，如果置信水平为 95% 的总体比例的置信区间为 (0.73, 0.81)，则这意味着总体比例在 73% 到 81% 之间的概率为 95%。

因此，比例的置信区间用于估计满足某些特征的总体比例的值。

正如我们将在下一节中看到的，比例的置信区间取决于样本比例和样本中的观测值数量。

比例的置信区间是通过从样本比例中添加和减去 Z _α/2的值乘以样本比例的平方根 (p) 乘以 1-p 再除以样本大小 (n) 来计算的。因此，计算比例置信区间的公式为：

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

金子：

$p$

是样本比例。
$n$

是样本大小。
$Z_{\alpha/2}$

是对应于 α/2 概率的标准正态分布的分位数。对于大样本量和 95% 置信水平，它通常接近 1.96；对于 99% 置信水平，它通常接近 2.576。

为了让您了解如何计算该比例的置信区间，我们在下面一步一步地为您提供了一个具体示例。

一家保险公司想要进行市场调查并确定一个国家有多少人拥有人寿保险。为此，我们对 700 人的随机样本进行了分析，得出的结论是，40% 的样本拥有人寿保险。该国人口比例在 95% 置信水平下的置信区间是多少？

为了确定总体比例的置信区间，我们需要使用上面看到的公式：

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

在这种情况下，我们希望置信区间的置信度为95%，因此我们需要取的Z _α/2值为1.96。

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

问题陈述已经告诉我们样本量为n=700，观察到的样本比例为p=0.40，因此我们将数据代入该比例的置信区间公式并计算区间的极限：

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

$\displaystyle \left(0,40-1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}}\ , \ 0,40+1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}\right)$

$\displaystyle \left(0,36 \ , \ 0,44\right)$

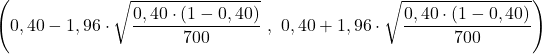
总之，研究人群的比例在 36% 到 44% 之间，置信度为 95%。

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多