不同分布的z分数比较

z 分数告诉您单个数据值与平均值的标准差有多少。计算方法如下：

z 分数 = (x – μ) / σ

金子：

• x：单个数据值
• μ：总体平均值
• σ：总体标准差

单个值的 z 分数可以解释如下：

• 正 z 分数：个体值高于平均水平。
• 负 z 值：个体值低于平均值。
• z 分数为 0：个体值等于平均值。

当我们想要比较两个不同分布的两个数据点的相对位置时，Z 分数特别有用。为了说明这一点，请考虑以下示例。

示例：比较 Z 分数

某大学考试的分数呈正态分布，平均值 μ = 80，标准差 σ = 4。杜安在这次考试中得分为 84。

另一场大学考试的分数呈正态分布，平均值 μ = 85，标准差 σ = 8。黛比在那次考试中得到了 90 分。

与他们自己的考试成绩分布相比，谁在考试中取得了最好的成绩？

为了回答这个问题，我们可以计算每个人的考试成绩的z分数：

Duane 的 z 分数 = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

黛比的 z 分数 = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0.625

Debbie 虽然得分较高，但与他特定考试的分布相比，Duane 的得分实际上更高。

要理解这一点，有助于形象化情况。以下是杜安的分数与他的特定考试细分的比较：

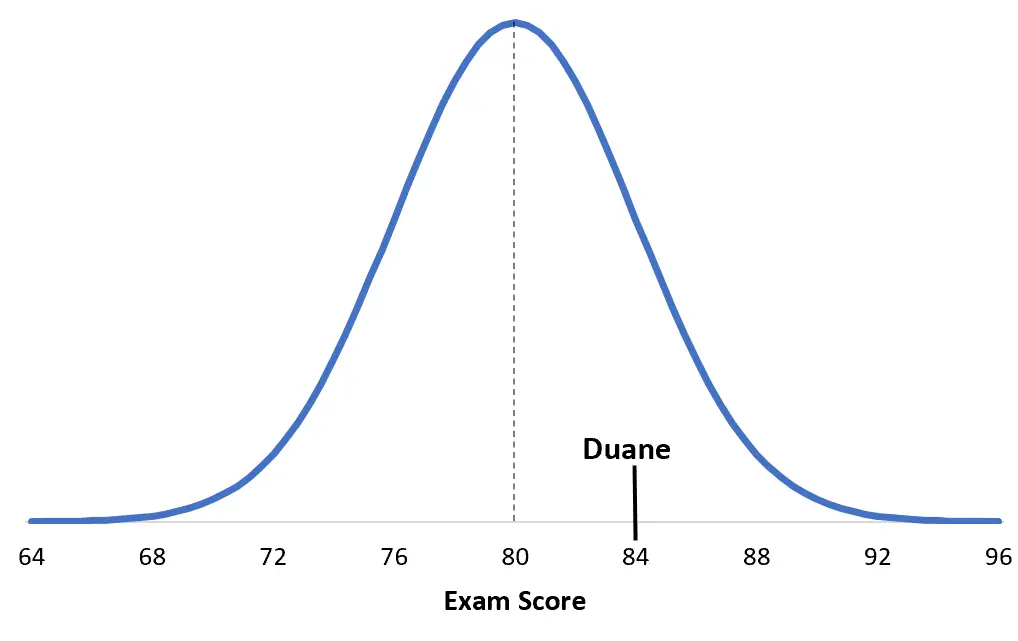
这是黛比的考试成绩：

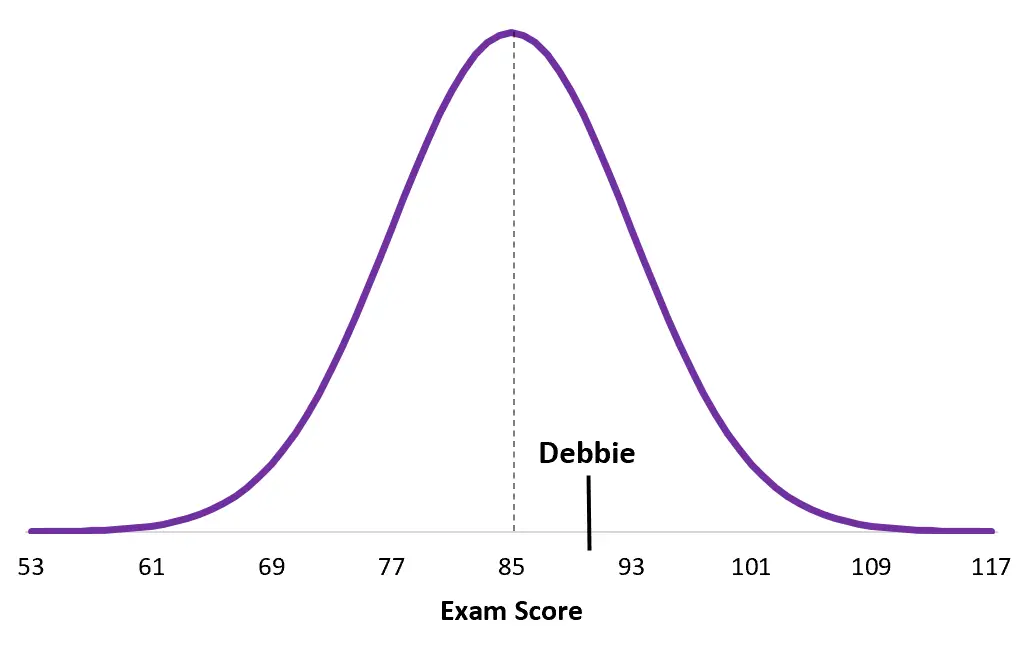
请注意，黛比的分数比杜安的分数更接近她的人口平均值。尽管她的总体分数较高，但她的 z 分数较低，仅仅是因为她特定考试的平均分数较高。

这个例子说明了为什么 z 分数对于比较不同分布的数据值如此有用：z 分数考虑了分布的均值和标准差，这使我们能够比较不同分布的数据值并查看哪个是与他们自己的发行版相比更高。

其他资源

Z 分数计算器
比较 Z 分数计算器