如何在 sas 中执行二比例 z 检验

双比例 z 检验用于确定两个总体比例之间是否存在统计显着差异。

该检验使用以下原假设：

• H ₀ : μ ₁ = μ ₂ (两者人口比例相等)

备择假设可以是双边的、左的或右的：

• H ₁ （双尾）： π ₁ ≠ π ₂ （两个群体比例不相等）
• H ₁ (左): π ₁ < π ₂ (人口1的比例小于人口2的比例)
• H ₁ (右): π ₁ > π ₂ (人口1的比例大于人口2的比例)

我们使用以下公式来计算 z 检验统计量：

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ )

其中 p ₁和 p ₂是样本比例，n ₁和 n ₂是样本大小，其中 p 是总合并比例，计算如下：

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ + n ₂ )

如果与 z 检验统计量对应的 p 值小于所选的显着性水平（常见选择为 0.10、0.05 和 0.01），则您可以拒绝原假设。

以下示例显示如何在 SAS 中执行二比例 z 检验。

示例：SAS 中的两个比例 Z 检验

假设我们想知道 A 县支持某项法律的居民比例与 B 县支持该法律的居民比例是否存在差异。

为了测试这一点，我们从每个县随机抽取了 50 名居民，并统计有多少人支持该法律。

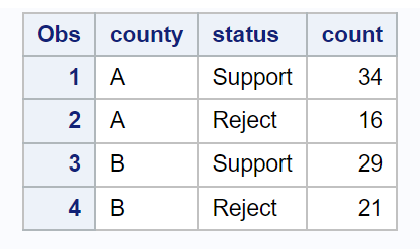
以下代码显示如何创建一个数据集，汇总每个县支持该法律的居民人数：

 /*create dataset*/
data my_data;
    input county $status $count;
    datalines ;
A Bracket 34
A Reject 16
B Bracket 29
B Reject 21
;
run ;

/*view dataset*/
proc print data =my_data;

然后，我们可以使用带有Riskdiff (equal var = null)选项的PROC FREQ语句来执行二比例 z 检验：

 /*perform two proportion z-test*/
proc freq data =my_data;
    weightcount ;
    county tables * status / riskdiff ( equal var = null);
run ; 

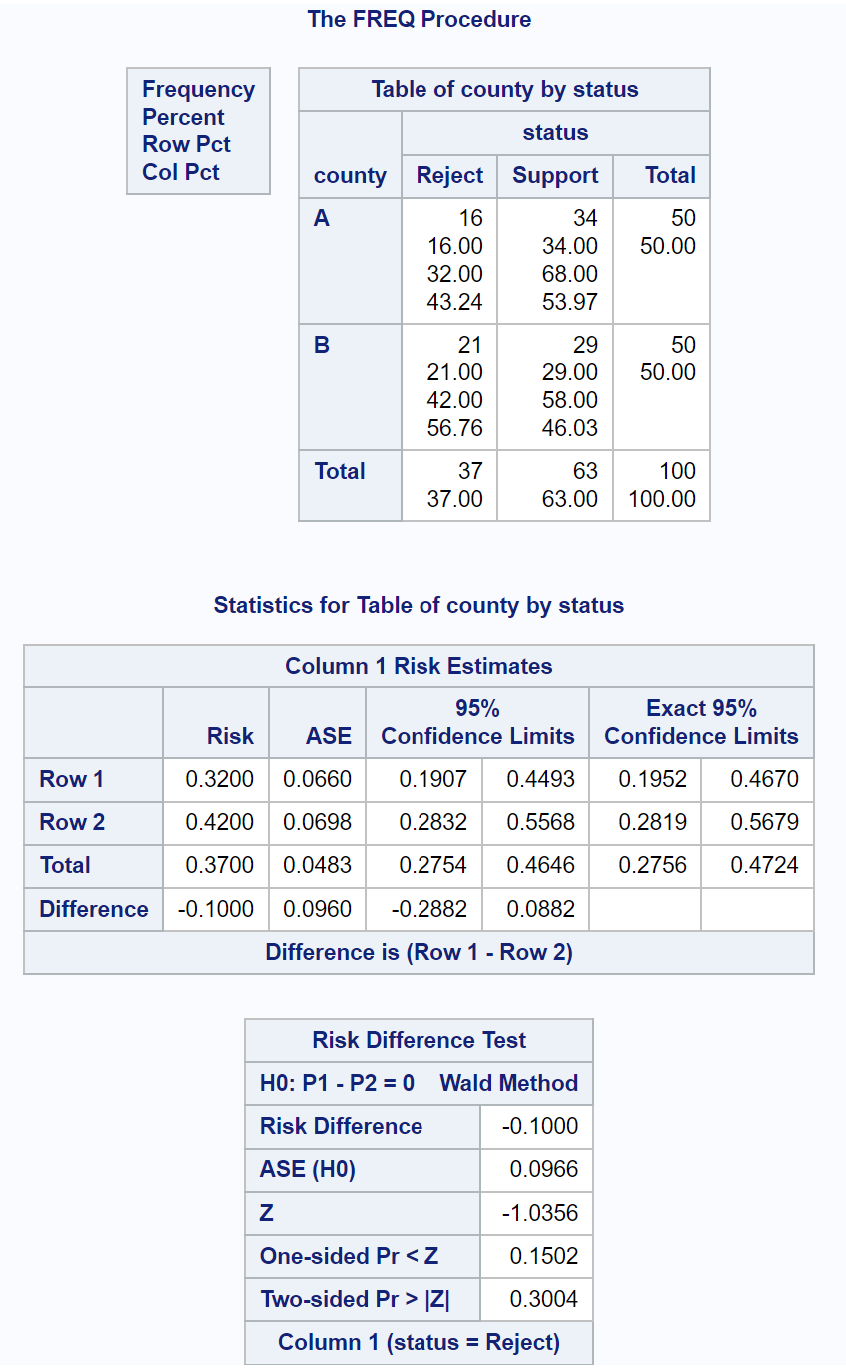
从结果表中的风险差异测试中，我们可以看到以下信息：

• Z 检验统计量： -1.0356
• 两侧 p 值： 0.3004

这个特定的二比例 z 检验使用以下假设：

• H ₀ : π ₁ = π ₂ (两者人口比例相等)
• H ₁ : π ₁ ≠ π ₂ (两者人口比例不相等)

由于输出中的 p 值不小于 0.05，因此我们无法拒绝原假设。

这意味着我们没有足够的证据表明两个县支持这项法律的居民比例不同。

其他资源

以下教程解释了如何在 SAS 中执行其他常见统计测试：

如何在 SAS 中执行单样本 t 检验
如何在 SAS 中执行双样本 t 检验
如何在 SAS 中执行配对样本 t 检验