如何在 sas 中执行怀特检验

怀特检验用于确定回归模型中是否存在异方差性。

异方差是指回归模型中响应变量不同水平上残差的离散程度不均匀，这违反了线性回归的关键假设之一，即残差在响应变量的每个水平上均匀分散。

本教程介绍如何在 SAS 中执行怀特检验以确定异方差是否是给定回归模型中的问题。

示例：SAS 中的白色测试

假设我们想要拟合一个多元线性回归模型，该模型使用学习时间和练习考试次数来预测学生的期末考试成绩：

考试成绩 = β ₀ + β ₁ （小时）+ β ₂ （预备考试）

首先，我们将使用以下代码创建一个包含 20 名学生信息的数据集：

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run ;

/*view dataset*/
proc print data =exam_data; 

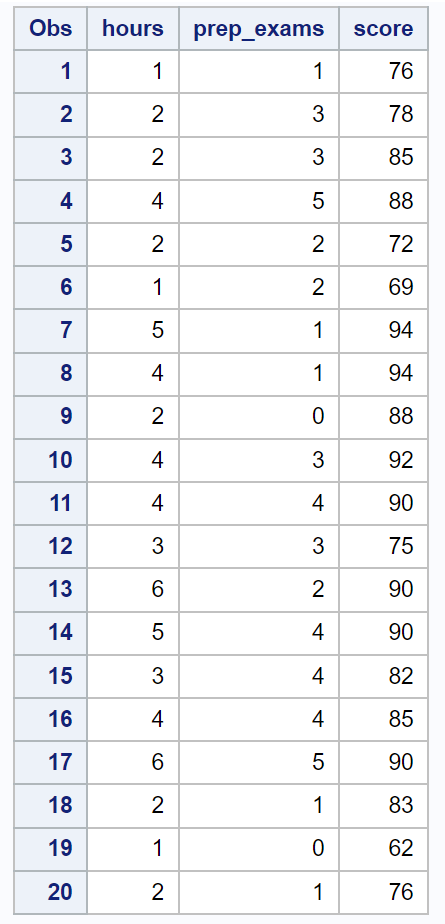
接下来，我们将使用proc reg来拟合这个多元线性回归模型，并使用spec选项来执行 White 异方差性检验：

 /*fit regression model and perform White's test*/
proc reg data =exam_data;
    model score = hours prep_exams / spec ;
run ;
quit ; 

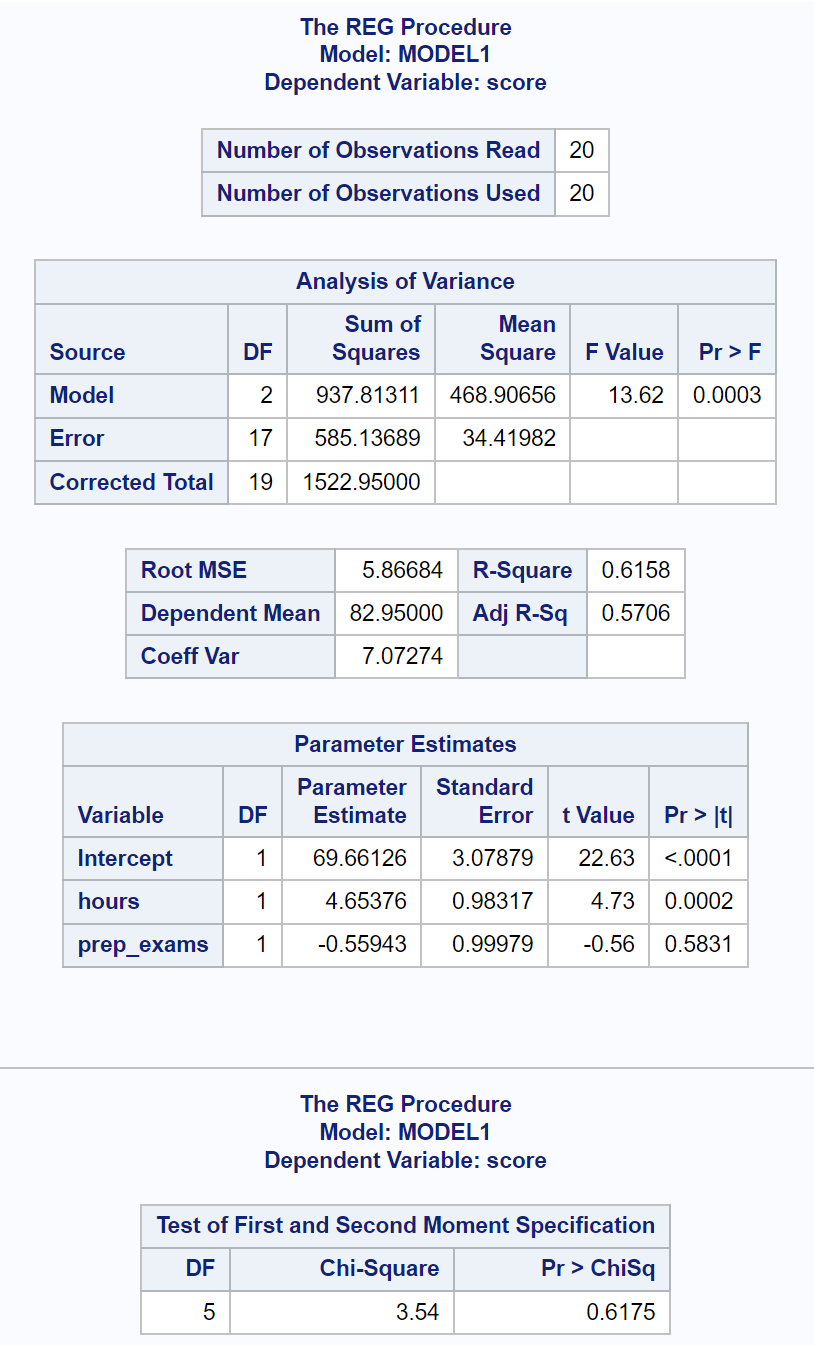
最后的结果表显示了怀特测试的结果。

从该表中，我们可以看到卡方检验统计量为3.54 ，相应的 p 值为0.6175 。

怀特检验使用以下原假设和备择假设：

• Null (H ₀ ) ：不存在异方差。
• 替代方案 ( _HA )：存在异方差。

由于 p 值不小于 0.05，因此我们无法拒绝原假设。

这意味着我们没有足够的证据来证明回归模型中存在异方差性。

因此，可以安全地解释回归汇总表中系数估计的标准误差。

接下来做什么

如果您未能拒绝怀特检验的原假设，则不存在异方差性，您可以继续解释原始回归的结果。

但是，如果拒绝零假设，则意味着数据中存在异方差性。在这种情况下，回归输出表中显示的标准误差可能不可靠。

有几种常见的方法可以解决此问题，包括：

1. 变换响应变量。您可以尝试对响应变量执行转换。

例如，您可以使用日志响应变量而不是原始响应变量。

一般来说，对响应变量取对数是消除异方差的有效方法。

另一种常见的转换是使用响应变量的平方根。

2. 使用加权回归。这种类型的回归根据拟合值的方差为每个数据点分配权重。

这为具有较高方差的数据点赋予较小的权重，从而减少了它们的残差平方。

当使用适当的权重时，可以消除异方差问题。