统计学中的点估计是什么？
在统计学中，我们通常感兴趣的是测量总体参数，即描述整个总体某些特征的数字。
两个最常见的总体参数是：
1、总体平均值：某个变量在总体中的平均值（例如某城市男性的平均身高）
2.人口比例：某个变量在人口中所占的比例（例如，一个县内支持某项法律的居民所占的比例）
即使我们想要测量这些参数，收集群体中每个个体的数据通常也过于昂贵且耗时。
相反，我们从总体中随机抽取样本，并使用样本数据来估计总体参数。
我们在样本中用来估计总体参数的数字称为点估计。这是我们对真实总体参数可能的最佳估计。
下表显示了我们用来估计总体参数的点估计：
| 的措施 | 人口参数 | 点估计 |
|---|---|---|
| 意思是 | μ（总体平均值） | x （样本平均值） |
| 部分 | π（人口比例） | p（样本比例） |
我们想要计算总体参数，但由于时间太长、成本太高，所以我们改为使用样本来计算点估计。
例如，假设我们想要估计佛罗里达州某种海龟的平均重量。由于佛罗里达州有数千只海龟，因此四处走动并单独称重每只海龟将非常耗时且昂贵。相反，我们可以抽取 50 只海龟的简单随机样本，并使用该样本中海龟的平均重量来估计真实的种群平均值：
如果样本平均值为 150.4 磅，那么我们对整个物种的真实种群平均值的点估计将为 150.4 磅。
代表性样本的重要性
当我们从总体中收集样本时，理想情况下我们希望样本类似于总体的“迷你版本”。
如果样本中个体的特征与总体中个体的特征密切匹配，则称该样本具有总体代表性。
当这种情况发生时，我们可以自信地将样本的结果推广到总体，并且我们可以说样本点估计是真实总体参数的无偏估计。
点估计和置信区间
尽管点估计代表了我们对真实总体参数的最佳估计，但它不太可能与总体参数完全对应。
在我们前面的例子中，不能保证样本中海龟的平均体重与整个种群中海龟的平均体重完全匹配。例如，我们可能会选择一个充满轻重量海龟的样本，或者可能选择一个充满重海龟的样本。
因此，为了捕捉这种不确定性，我们可以创建一个置信区间——可能包含具有一定置信水平的总体参数的一系列值。
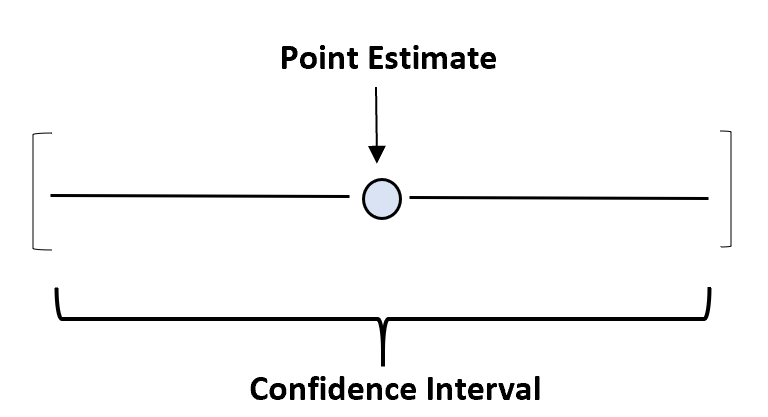
例如，我们可以使用 150.4 磅的样本平均值来估计海龟物种的真实平均重量。我们的置信区间将是一个值范围——也许是 145 磅到 155.8 磅。
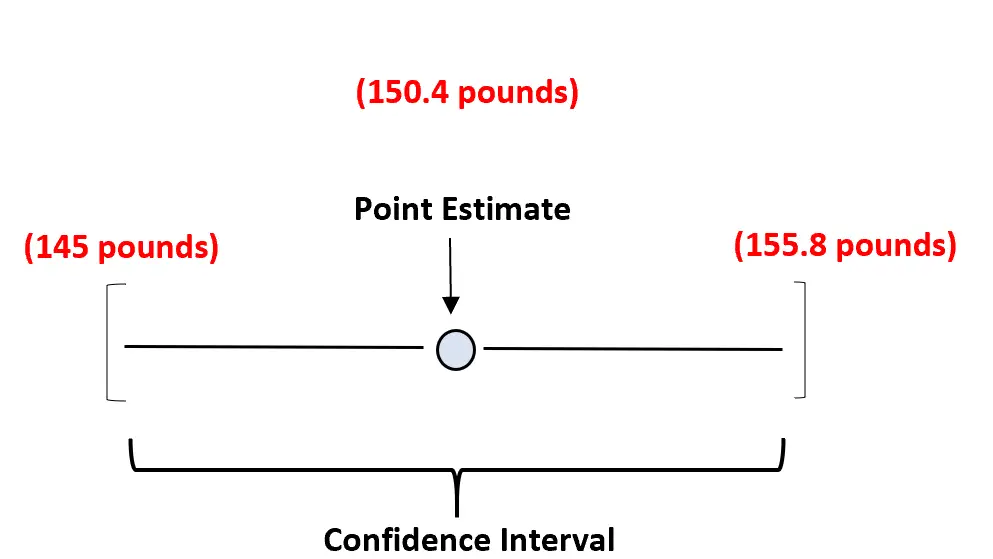
我们的点估计是对真实平均总体权重的最佳估计，置信区间提供了可能包含真实平均总体权重的一系列值。
您可以在此处了解有关置信区间的更多信息。
其他资源
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多