皮尔逊相关系数
本文解释什么是皮尔逊相关系数(或线性相关系数)及其用途。您将通过逐步练习了解如何计算皮尔逊相关系数。此外,您还可以使用最后的在线计算器找到任何数据集的皮尔逊相关系数值。
什么是皮尔逊相关系数?
皮尔逊相关系数,也称为线性相关系数或简称相关系数,是指示两个变量之间关系的统计度量。
要计算两个变量之间的皮尔逊相关系数,必须将所述变量的协方差除以它们方差乘积的平方根。
因此,皮尔逊相关系数试图量化两个定量随机变量之间的线性相关性。先验地,以数值方式评估变量之间的相关性是很复杂的,因为很难确定变量对之间的相关性是否更强,如果(如在 pues 中),皮尔逊相关系数的目的是评估变量之间的关系,以便能够他们之间进行比较。
Pearson 相关指数的值介于 -1 和 +1 之间(包括 -1 和 +1)。我们将在下面看到如何解释皮尔逊相关系数的值。
皮尔逊相关系数公式
两个统计变量的皮尔逊相关系数等于变量的协方差与每个变量的方差乘积的平方根之间的商。
因此,皮尔逊相关系数的计算公式如下:
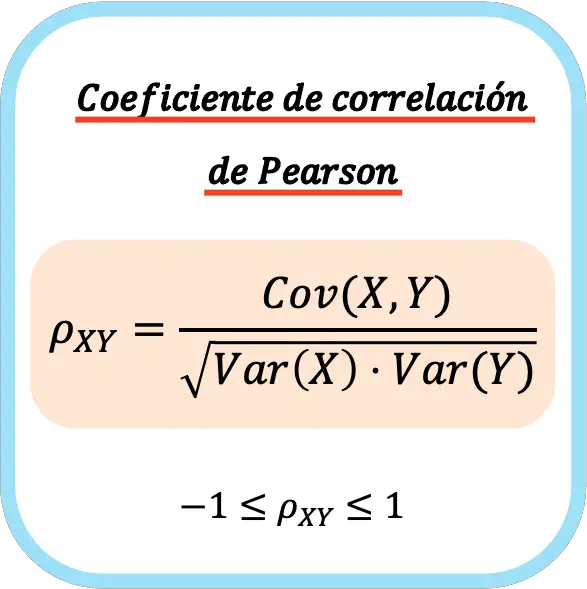
👉您可以使用下面的计算器计算任何数据集的皮尔逊相关系数。
当对总体计算皮尔逊相关系数时,通常用希腊字母ρ表示。但当相对于样本计算系数时,通常使用字母r作为符号。
请记住,要确定皮尔逊相关系数,您必须知道如何计算两个变量之间的协方差和变量的方差。此外,您需要了解这些统计指标的含义。因此,在继续讲解之前,建议先阅读以下两篇文章:
计算 Pearson 相关系数的示例
考虑到皮尔逊相关系数的定义及其公式,下面是一个分步示例,您可以了解它是如何计算的。
- 计算以下两个连续变量之间的皮尔逊相关系数:

在计算皮尔逊相关系数之前,我们将数据集用散点图表示来分析两个变量之间的关系:
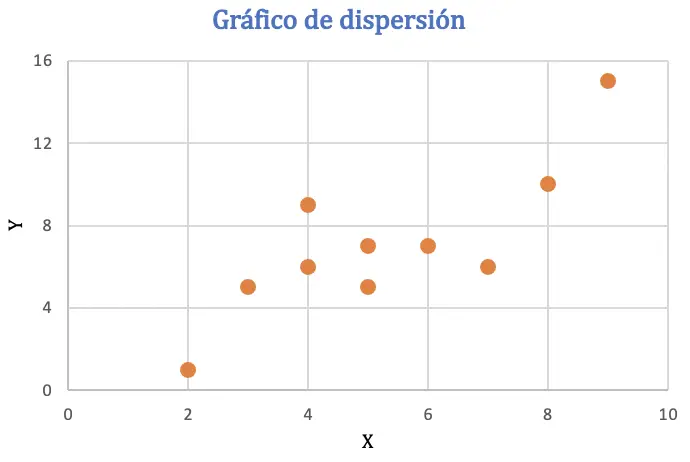
从散点图可以推断,数据可能呈正趋势,或者换句话说,当一个变量的值增加时,另一个变量也会增加。为了检查相关性,我们将找到皮尔逊系数。
首先要做的是分别找到每个变量的算术平均值,这相当于数据的总和除以观测值的数量。
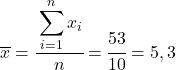
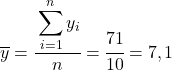
现在我们知道每个变量的平均值,我们需要将以下列添加到数据表中:
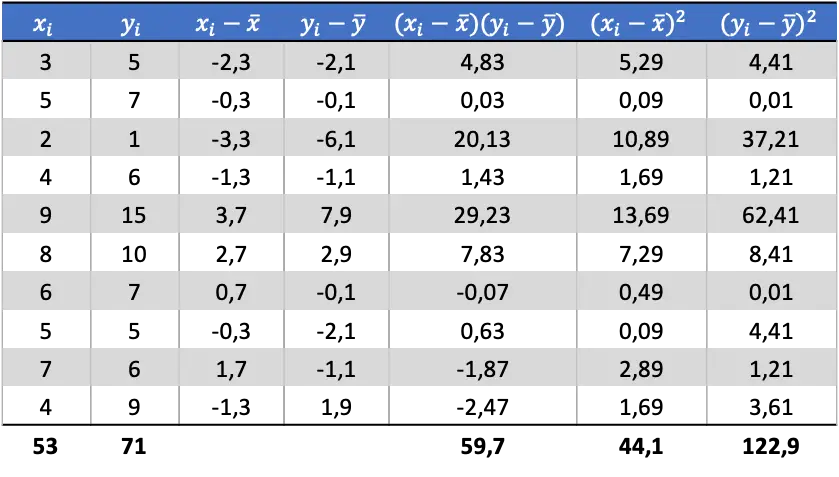
根据表中计算的数据,我们确定协方差和方差的值(如果您不记得这是如何完成的,上面有两个链接详细解释了这一点):
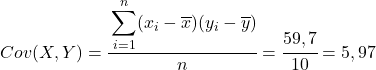
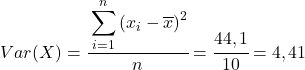
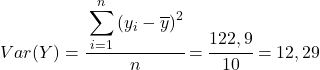
最后,简单应用皮尔逊相关系数公式即可得到其值:
![]()
Pearson 相关系数的值非常接近 1,这意味着这两个变量具有相当强的正相关性。
正如您所看到的,为了确定 Pearson 相关系数,使用 Excel 等程序更快地执行列计算非常有用。
皮尔逊相关系数计算器
在下面的计算器中输入一组统计数据,计算两个变量之间的皮尔逊相关系数。您需要分隔数据对,以便第一个框中只有一个变量的值,第二个框中只有第二个变量的值。
数据必须用空格分隔,并使用句点作为小数点分隔符输入。
解释皮尔逊相关系数
在本节中,我们将看到如何解释皮尔逊相关系数,因为仅仅知道它的值是不够的,但你必须知道如何分析它的含义。
因此,皮尔逊相关系数的解释取决于其值:
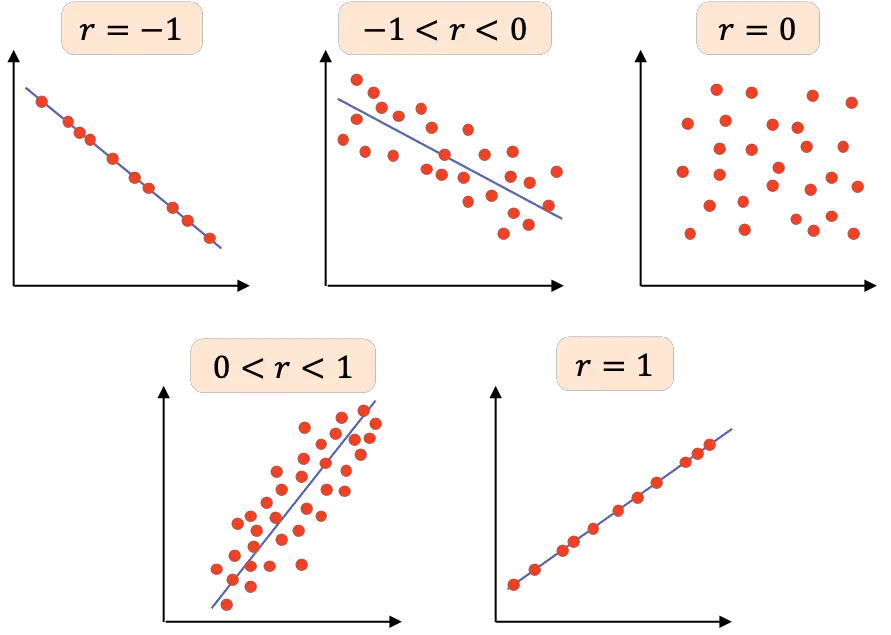
- r=-1 :两个变量具有完美的负相关性,因此我们可以画一条负斜率的线,将所有点连接起来。
- -1<r<0 :两个变量之间的相关性为负,因此当一个变量增加时另一个变量减少。该值越接近-1,变量负相关程度越高。
- r=0 :两个变量之间的相关性很弱,实际上它们之间的线性关系为零。这并不意味着变量是独立的,因为它们可能具有非线性关系。
- 0<r<1 :两个变量之间的相关性为正,值越接近+1,变量之间的相关性越强。在这种情况下,当另一个变量的值也增加时,一个变量的值往往会增加。
- r=1 :两个变量具有完美的正相关性,即呈正线性关系。
综上所述,下表列出了皮尔逊相关系数的不同解释:
| 价值 | 解释 |
|---|---|
| r=-1 | 完美的负相关。 |
| -1<r<0 | 负相关:相关性越接近-1,相关性越强。 |
| r=0 | 零线性相关。 |
| 0<r<1 | 正相关:相关性越接近+1,相关性越强。 |
| r=1 | 完美的正相关。 |
请记住,即使两个变量之间存在关系,也不意味着它们之间存在因果关系,即两个变量之间的相关性并不意味着某个变量的变化是该变量变化的原因。其他变量。
例如,如果我们发现体内两种不同激素的产生之间存在正相关关系,那么一种激素的增加不一定会导致另一种激素的增加。身体可能会产生这两种激素,因为它需要这两种激素来对抗疾病,因此同时增加了这两种激素的水平,在这种情况下,原因就是疾病。为了确定这两种激素之间是否存在因果关系,需要进行进一步的研究。