相对频率
在本文中,您将了解什么是统计学中的相对频率、如何获得相对频率以及两个逐步解决相对频率的练习。
什么是相对频率?
在统计学中,相对频率是一种度量,以比例或百分比的形式指示某个值在数据样本中出现的次数。更准确地说,相对频率等于绝对频率除以数据总数。
例如,如果某个值的绝对频率为 15,并且总共有 100 个数据点,则该值的相对频率为 0.15 (15/100=0.15)。
一般用符号hi来表示相对频率。虽然统计界还没有达成共识,所以你可以看到用另一个符号代表的相对频率。
如何计算相对频率
相对频率等于绝对频率除以数据总数。因此,要计算相对频率,必须首先找到绝对频率,然后将其除以观测总数。
因此,相对频率的计算公式如下:
![]()
金子:
-
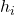
是相对频率。
-

是绝对频率。
-

是数据总数。
另一方面,要计算以百分比表示的相对频率,即以百分比表示的相对频率,只需将前面的公式乘以 100:
![]()
相对频率的例子
一旦您了解了相对频率的定义,下面是两个实际示例,您可以了解如何计算此类频率。在第一个示例中,确定离散变量的相对频率,在第二个示例中,确定连续变量的相对频率。
示例1:离散变量
- 班级 30 名学生的统计科目成绩如下。每个音符的相对频率是多少?
![]()
![]()
![]()
本练习中的变量是离散的,因为数据只能是整数;因此,无需将数据分组。
为了找到相对频率,我们必须首先确定绝对频率。因此,我们构建一个频率表并计算每个不同值的绝对频率:

现在我们已经计算了绝对频率,我们可以计算相对频率。为此,只需将每个绝对频率除以数据总数 (30):
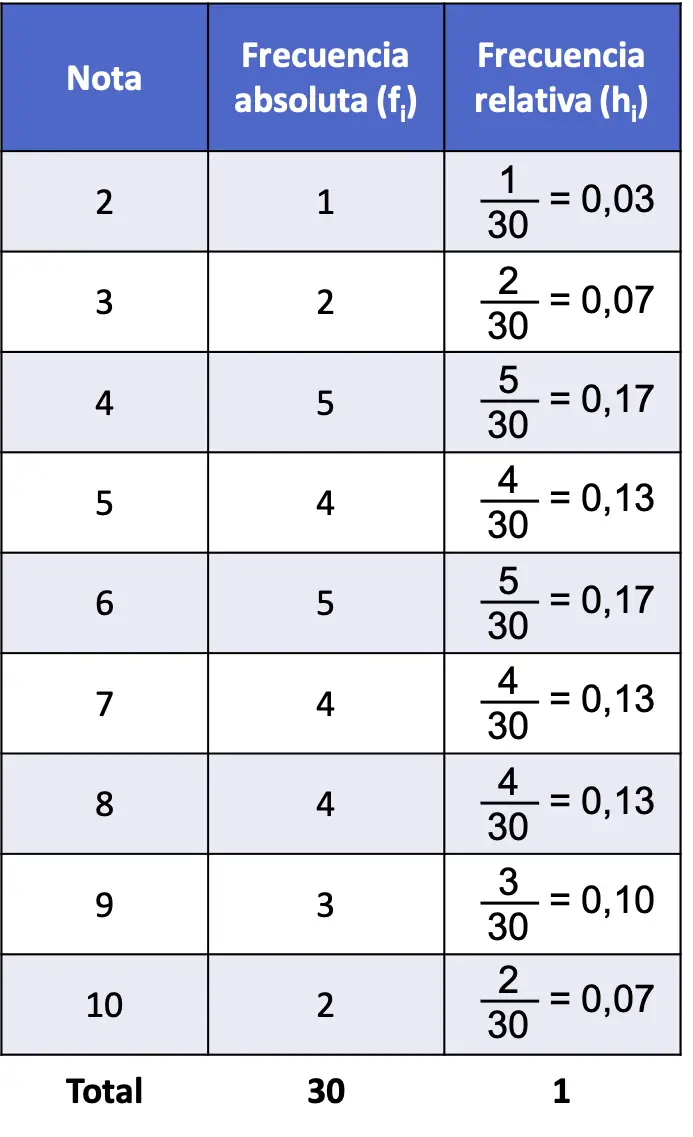
那么,绝对频率和相对频率问题的频率表如下:

请注意,所有相对频率的总和始终为 1,否则这意味着某些计算是错误的。
示例 2:连续变量
- 测量了 20 个人的身高,得到如下结果。将数据分成多个区间并找出每个区间的相对频率。
![]()
![]()
该统计样本中的数据属于连续变量,因为它们是十进制的,因此变量可以取任何值。因此,在进行频率计算之前,我们首先将数据分组为幅度为十分之十的区间。
接下来,我们制作一个频率表,其中包含每个区间的绝对频率:

一旦我们找到了绝对频率,我们就可以通过将每个区间的绝对频率除以数据总数(20)来得到每个区间的相对频率:

累积相对频率
顾名思义,累积相对频率是统计中使用的另一种频率,根据相对频率计算得出。
更准确地说,某个值的累积相对频率等于该值本身的相对频率加上所有较小值的相对频率之和。
为了让您了解如何获得累积相对频率,第一个示例中的数据集的累积相对频率已计算如下:
