肖文内标准：定义和示例

异常值是与数据集中的其他值异常远离的观察值。异常值可能会产生问题，因为它们会影响分析结果。

识别数据集中异常值的一种方法是使用Chauvenet 准则，该准则使用以下过程：

1.对于数据集中的每个单独值 x _i ，计算与平均值的偏差，如下所示：

偏差 = |x _i – x | /秒

其中x是样本均值， s是样本标准差。

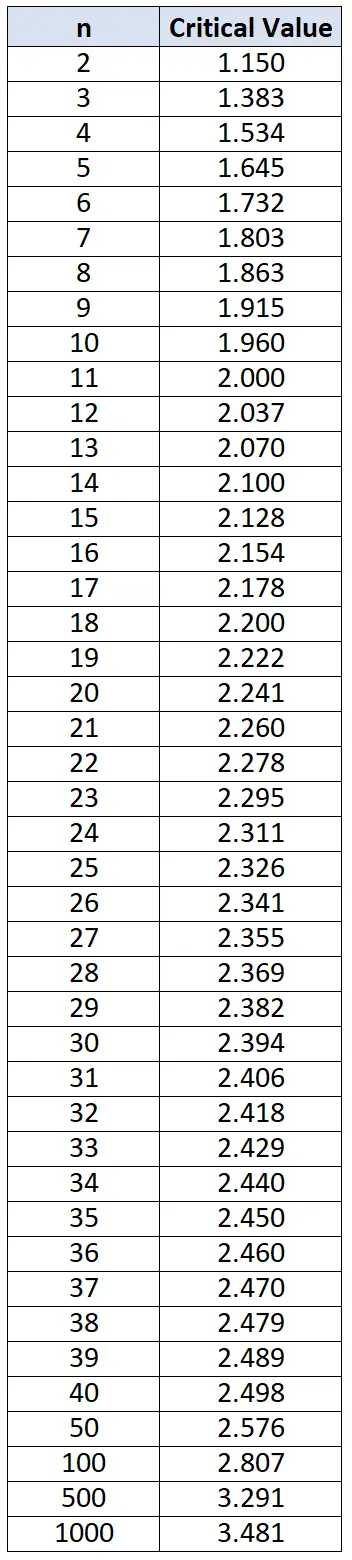
2.将每个单独值的偏差与下面肖文标准表中的临界值进行比较。对于偏差大于表中发现的偏差的单个数据值，将这些数据值报告为异常值。

肖文内准则：一个例子

假设我们有以下包含 15 个值的数据集：

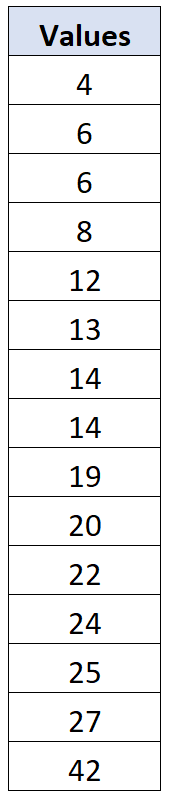
该数据集的样本平均值为x = 17.067 ，样本标准差为s = 10.096 。对于每个单独的数据值，我们可以计算其偏差如下：

偏差 = |x _i – x | /秒

例如：

• 第一个数据值的偏差为 |4 – 17.067| / 10,096 = 1,294 。
• 第一个数据值的偏差为 |6 – 17.067| / 10.096 = 1.096 。

等等。

我们可以使用相同的公式来计算每个单独数据值的偏差：

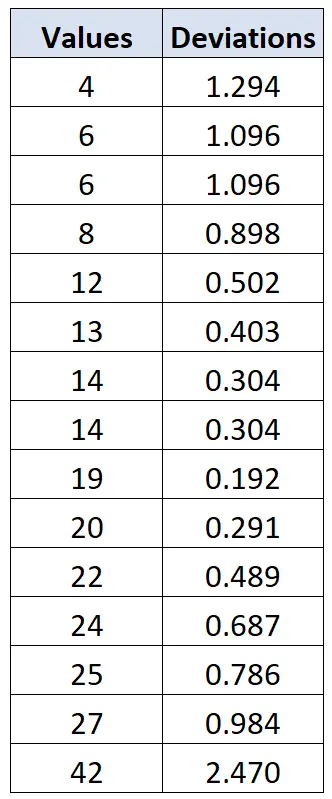
然后我们可以参考 Chauvenet 标准表，并注意到对应于 n=15 的样本量的临界值为2.128 。因此，任何偏差大于 2.128 的值都可以被视为异常值。

结果发现值42的偏差大于 2.128：

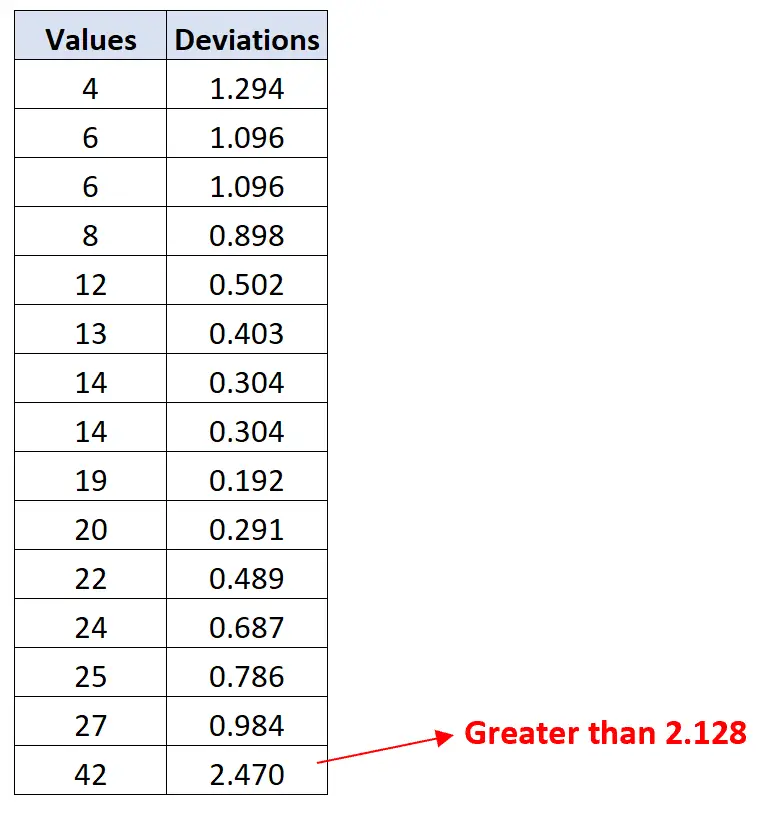
因此，值 42 是该数据集中唯一的异常值。

使用肖文内准则的注意事项

Chauvenet 准则假设数据集中的值呈正态分布。如果不满足此假设，则使用肖文内准则来识别异常值可能无效。

如果您使用此方法并发现某个值是异常值，则必须首先验证该值是否不是数据输入错误的结果。有时，数据只是输入错误。

如果该值确实是异常值，并且会对您的整体分析产生重大影响，则您可以选择将其删除。请务必在报告结果时提及您删除了异常值。

此外，此方法只能在给定数据集上使用一次。例如，假设我们使用此标准将值42识别为上一个示例中的异常值，并从数据集中删除该值。

那么我们不应该重新计算样本均值和样本标准差并再次计算偏差以找到更多异常值。