如何在 stata 回归中使用稳健标准误差
多元线性回归是一种我们可以用来理解多个解释变量和响应变量之间关系的方法。
不幸的是,回归中经常出现的一个问题被称为异方差,其中残差的方差在一系列测量值上存在系统性变化。
这导致回归系数估计的方差增加,但回归模型没有考虑到这一点。这使得回归模型更有可能声称模型中的某个项具有统计显着性,而实际上并非如此。
解决此问题的一种方法是使用稳健标准误差,它对于异方差问题更加“稳健”,并且往往能够更准确地测量回归系数的真实标准误差。
本教程介绍如何在 Stata 回归分析中使用稳健标准误差。
示例:Stata 中的稳健标准误
我们将使用自动集成的 Stata 数据集来说明如何在回归中使用稳健的标准误差。
步骤1:加载并显示数据。
首先,使用以下命令加载数据:
系统自动使用
然后使用以下命令显示原始数据:
br
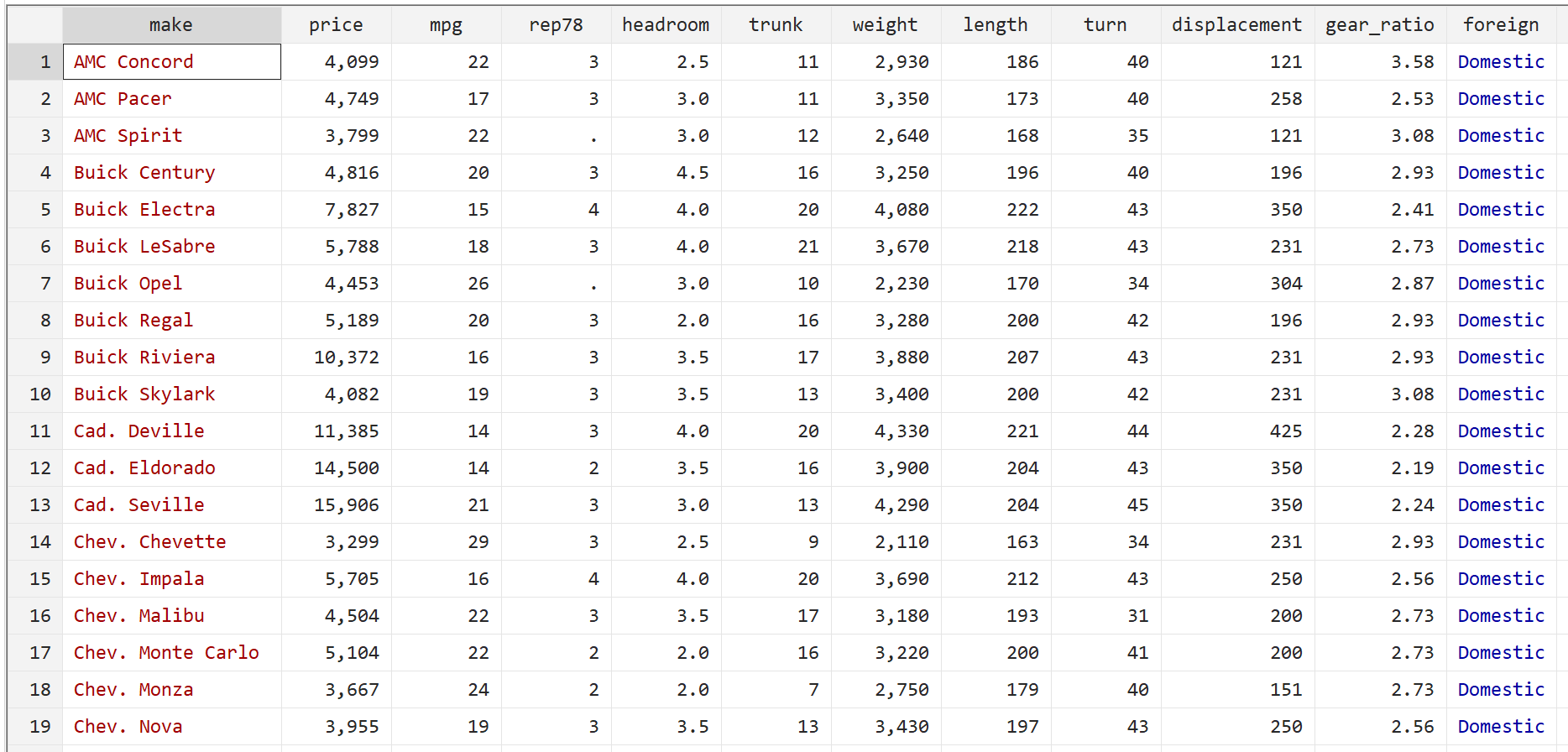
步骤 2:执行没有稳健标准误差的多元线性回归。
接下来,我们将输入以下命令来执行多元线性回归,使用价格作为响应变量, mpg和体重作为解释变量:
回归价格 mpg 重量

步骤 3:使用稳健标准误差执行多元线性回归。
我们现在将执行完全相同的多元线性回归,但这次我们将使用vce(robust)命令,以便 Stata 知道如何使用稳健标准误差:
回归价格 mpg 重量,vce(稳健)
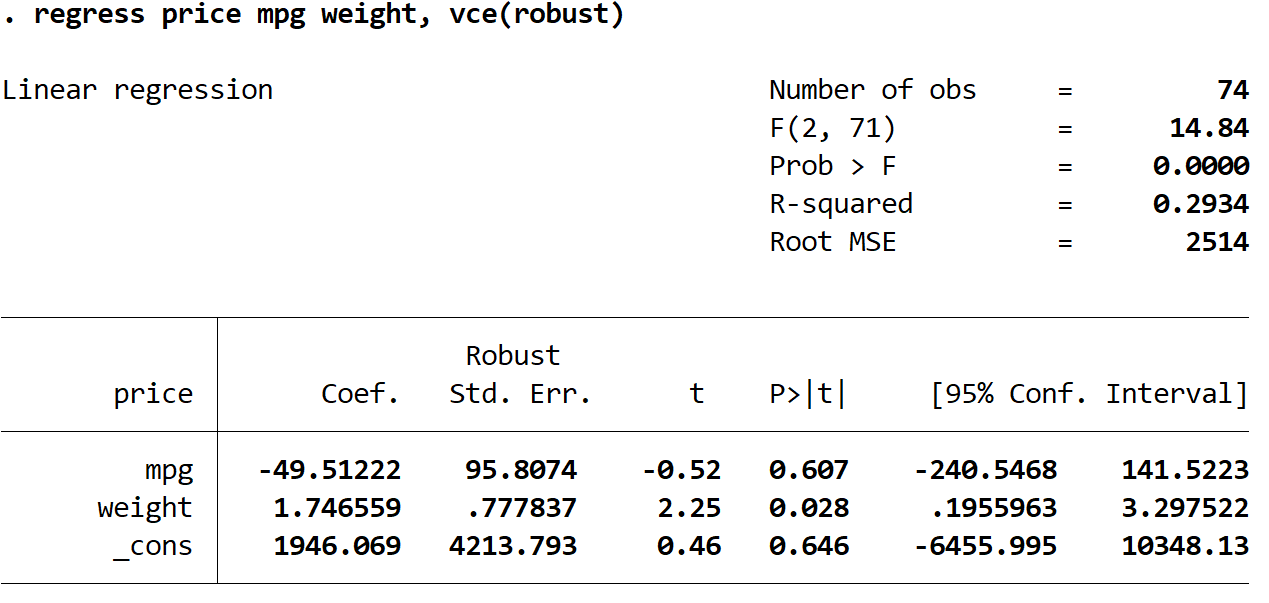
这里有一些有趣的事情需要注意:
1. 系数估计值保持不变。当我们使用稳健的标准误差时,系数估计值根本不会改变。请注意,两个回归的 mpg、体重和常数的系数估计如下:
- 英里/加仑: -49.51222
- 重量: 1.746559
- _反对: 1946.069
2. 标准误发生了变化。请注意,当我们使用稳健标准误差时,每个系数估计值的标准误差都会增加。
注意:在大多数情况下,稳健标准误差将大于正常标准误差,但在极少数情况下,稳健标准误差实际上可能会更小。
3、各系数的检验统计量发生了变化。请注意,每个检验统计量t的绝对值均已减小。实际上,检验统计量的计算方式为估计系数除以标准误差。因此,标准误差越大,检验统计量的绝对值越小。
4. p值发生了变化。请注意,每个变量的 p 值也增加了。这是因为较小的检验统计量与较大的 p 值相关。
尽管我们的系数的 p 值发生了变化,但mpg变量在 α = 0.05 时仍然不具有统计显着性,并且变量权重在α = 0.05 时仍然具有统计显着性。