简单随机抽样

经过本杰明·安德森博 8月 6, 2023 统计数据 0 条评论

在本文中，您将了解什么是简单随机样本以及简单随机样本有哪些类型。此外，我们还通过示例解释了如何进行简单随机抽样。最后，您将能够了解简单随机抽样的优点和缺点。

什么是简单随机抽样？

在统计学中，简单随机抽样是一种用于选择研究样本的概率方法。简单随机抽样的主要特点是它为统计总体中的每个元素提供了包含在研究样本中的相同概率。

在简单随机抽样中，样本元素是随机选择的，因此得到的样本是完全随机的。

因此，使用简单随机抽样，获得给定样本的概率等于获得任何其他样本的概率。我们将在下面看到这个概率是如何计算的。

请记住，还有其他方法可以从样本中选择个体。最常用的抽样类型主要有：

简单随机抽样
分层抽样
系统抽样
整群抽样

简单随机抽样的概念当然是最容易理解的类型，但有时恰恰由于其随机性，它的实现起来是最复杂的。

如何进行简单随机抽样

进行简单随机抽样的步骤如下：

列出人口的所有要素。
为总体中的每个元素分配一个序号(1, 2, 3,…, n)。
设置所需的样本大小。
使用随机数生成器生成与所选样本大小一样多的数字。
分配给生成编号的个体是被选为样本一部分的个体。

生成随机数有多种方法，最传统的是抽签法和数表法：

抽奖方法是将所有号码放入一个盒子中，将它们洗牌，然后随机抽取号码。
数表法涉及从包含所有可能数字的表中随机选择数字。

尽管您也可以使用前两种方法中的任何一种，但这些方法需要更多时间并且更适合较小的样本量。目前，计算机程序用于更快地生成随机数，例如您可以使用Excel程序。

另一方面，您必须考虑到样本量必须足够，以便尽可能减少抽样误差。找到理想的样本量并非易事。如果您对此有任何疑问，可以在我们的网站上搜索我们解释如何执行此操作的文章。

简单随机抽样示例

一旦我们了解了简单随机抽样的定义，我们就会看到如何执行此类抽样的已解决示例。

例如，如果一家公司有 2000 名员工，我们想要对 400 名员工进行样本统计研究，通过简单随机抽样来选择样本中的个体，首先要做的事情包括为每个员工分配一个从 1 到 2000 的数字。

号码分配完毕后，我们需要随机选择400个号码。这种情况下样本量相当大，所以最好使用Excel等计算机软件。

然后，被选中参加研究的 400 名工人将是上一步中确定的分配人数。

在此示例中，400 个项目被认为是具有足够代表性的样本量，但从逻辑上讲，这个数字会根据实验而变化。

简单随机抽样的类型

简单随机抽样有两种类型：

带放回的简单随机抽样：返回抽样框中选定的元素并可以再次选择。
无放回的简单随机抽样：被选为样本一部分的项目将被删除，并且不能再被选择。

带放回的简单随机抽样是最简单的抽样类型，因为总是重复完全相同的过程来从样本中选择项目。然而，无放回的简单随机抽样由于更精确而被更广泛地使用。下面将更详细地解释这两种类型。

带放回的简单随机抽样

带放回的简单随机抽样涉及将每个选定项目返回到抽样框，以便存在再次选择它的可能性。

因此，有可能获得单个项目被多次选择的样本，尽管这显然不太可能。

从数学上讲，这是一种非常简单的采样类型，因为每次提取的概率是相同的。这就是为什么通常先于其他人开始研究这种采样技术的原因。

在放回的简单随机抽样中，获得一定顺序样本的概率可以使用以下公式计算：

$P=\cfrac{1}{N^n}$

是

$N$

人口总数和

$n$

将执行的独立提取的数量。

另一方面，当顺序无关紧要时，获得样本的概率使用以下表达式计算：

$P=\cfrac{n!}{\displaystyle N^n\prod_{i=1}^z k_i!}$

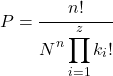
金子

$n$

是独立提取的数量，

$z$

样本中不同元素的数量和

$k_i$

您希望该项目出现多少次

$i$

在样本中。

最后求该元素包含的概率

$i$

，也就是说包含该元素的概率

$i$

在示例中，应使用以下公式：

$\displaystyle \pi_i=1-\left(1-\frac{1}{N}\right)^n$

简单随机抽样，无需放回

无放回的简单随机抽样涉及从样本中选择与所需样本大小相同的个体，以便每个个体一旦被选择就不能被再次选择。因此，每个选定的项目都会被删除而不是被替换。

当我们谈论简单随机抽样时，我们通常指的是不替换个体的抽样，因为它是实践中最常用的抽样。

为了确定在放回的简单随机抽样中获得一定顺序样本的概率，使用以下公式：

$P=\cfrac{1}{n!\begin{pmatrix}N\\n\end{pmatrix}}$

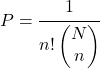
是

$N$

总体中的元素总数和

$n$

要执行的相关提取的数量。

另一方面，如果不考虑提取顺序，则获得样本的概率等于：

$P=\cfrac{1}{\begin{pmatrix}N\\n\end{pmatrix}}$

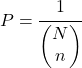
最后，通过应用拉普拉斯规则计算在简单随机抽样中不放回地包含元素的概率：

$\displaystyle \pi_i=\frac{n}{N}$

简单随机抽样的优点和缺点

简单随机抽样有以下优点和缺点：

优势	缺点
容易明白。	人口所有要素的清单是必要的。
所有可能的样本都是等概率的。	对于大样本量来说，这可能非常昂贵。
通常会获得代表性样品。	它往往有较大的抽样误差。
进行采样不需要任何技术知识。	研究人员在所研究领域可能拥有的知识没有被利用。
允许您快速计算平均值和偏差。	如果样本太小，可能不具有代表性。
有统计软件可以分析数据。	不适合需要个人访谈的研究。

正如我们所看到的，简单随机抽样的主要特征之一是它易于理解和解释。事实上，进行采样的人不需要是分析领域的专家。然而，这既是优点也是缺点，因为在其他类型的采样中，可以利用分析师的知识来实现更好的采样。

同样，由于抽样是随机的，因此与其他类型的抽样不同，采用这个或那个元素构成研究样本的概率是等概率的。

尽管通常会获得总体的代表性样本，但与其他类型的抽样相比，简单随机抽样的抽样误差较大。此外，如果个体规模很小，样本甚至可能不具有代表性。

简单随机抽样的一个非常有吸引力的特性是它可以使用计算机程序进行，从而可以快速进行统计计算。

最后，应该指出的是，简单随机抽样可能比其他类型的抽样更昂贵，特别是在广泛分散的人群中，因为它可能需要使用更多的资源进行研究。例如，由于是随机抽样，被选中进行研究的人可能在地理上分散得很远，因此进行面对面访谈的成本会高得多。

关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多