统计人口
在本文中,我们解释什么是统计人口。您将找到统计总体的几个示例、存在的不同类型的总体以及最后统计中总体和样本之间的区别。
什么是统计人口?
在统计学中,总体是一组具有相似特征的元素,旨在对其进行统计研究。
这个概念可以互换地称为统计总体或简称总体。
接下来,总体规模,也称为总体规模,是您要研究的群体中的元素总数。
人口统计举例
考虑到统计总体的定义,我们将看到几个总体示例,以更好地理解其含义。
例如,当我们对某个班级的学生在一年内取得的成绩进行研究时,该班级的学生就构成了该研究的统计总体。
再比如,如果要对某个工厂在给定时期内生产的零件质量进行统计分析,则该工厂在该时期内生产的所有零件就构成了研究的总体。
最后,当在一个领土上进行统计时,该领土的居民也是统计人口,例如在计算一个国家的预期寿命时,该国家的居民代表该研究的统计人口。
统计人口类型
统计人口有两种类型:
- 有限统计总体:元素数量有限,即可以统计的总体。
- 无限统计总体:元素数量无限的总体,即没有尽头。
例如,一天中在道路上行驶的汽车数量构成有限人口,因为即使数量非常大,也是可数的。相反,宇宙中行星的数量构成了无限的人口,因为并非所有行星都尚未被发现,因此无法计算。
您应该记住,对统计总体类型进行分组的方法有很多,也可以根据变量分为定性总体和定量总体。但通常,在有限总体和无限总体之间进行大分类。
统计总体及样本
最后,我们将看到总体和样本的概念在统计中有何不同,因为它们是通常齐头并进的两个术语。
在统计学中,总体与样本之间的差异是相对于研究中元素总数的比例。统计总体是进行研究的所有要素,然而,统计样本是研究所有要素的一部分。
因此,样本的大小将始终小于或等于总体的大小。
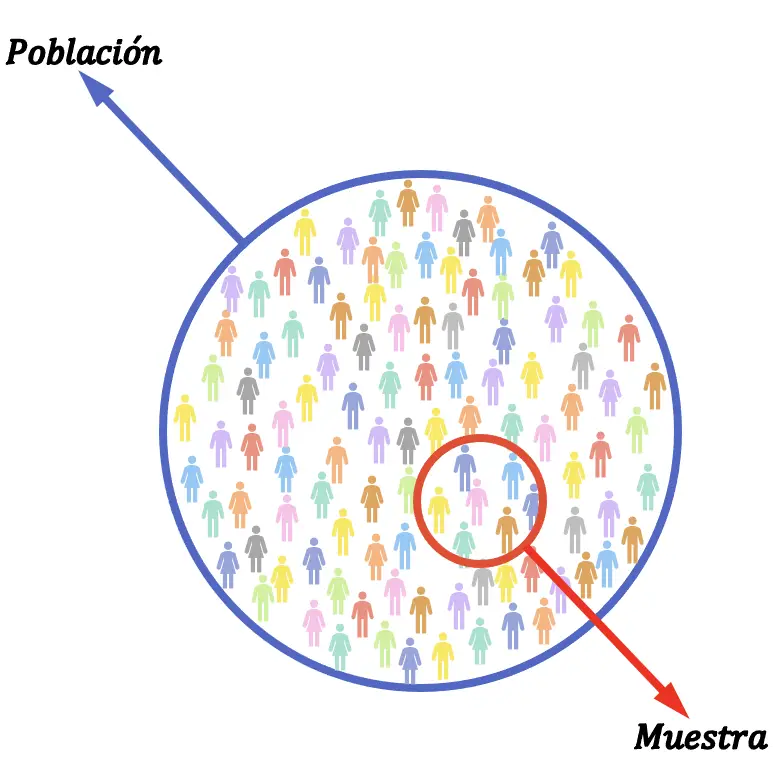
统计样本也可以称为总体的子集。
通常,为了对总体进行统计研究,不会从总体的每个元素中获取数据,而是选择具有代表性的样本,对样本进行研究,然后将研究结果外推到整个总体。人口。
例如,当你想做市场调查时,你不会询问所有对你的产品感兴趣的人,你只调查一部分,然后用收集到的数据来研究市场。
需要注意的是,统计研究的样本量(sample size)的确定并不简单,因为样本量越大,越能代表总体,但样本量越大,分析就越复杂将。因此需要更多的资源和资金。