Socs:描述分布的有用缩写
在统计学中,我们经常想了解一组数据是如何分布的。特别是,关于发行版,了解以下四件事是有用的:
1 .形状
- 分布是对称的还是偏向一侧?
- 分布是单峰(一个峰)还是双峰(两个峰)?
2. 异常值
- 分布中是否存在异常值?
3. 中心
- 均值、中位数和分布模式是什么?
4.传播
- 分布的极差、四分位距、标准差和方差是多少?
SOCS是一个有用的缩写词,我们可以用它来记住这四件事。它的意思是“形状、异常值、中心、分布”。
让我们通过一个简单的示例来了解如何使用 SOCS 来描述分布。
示例:如何使用 SOCS 描述分布
假设我们有以下数据集,显示 20 种不同植物样本的高度。
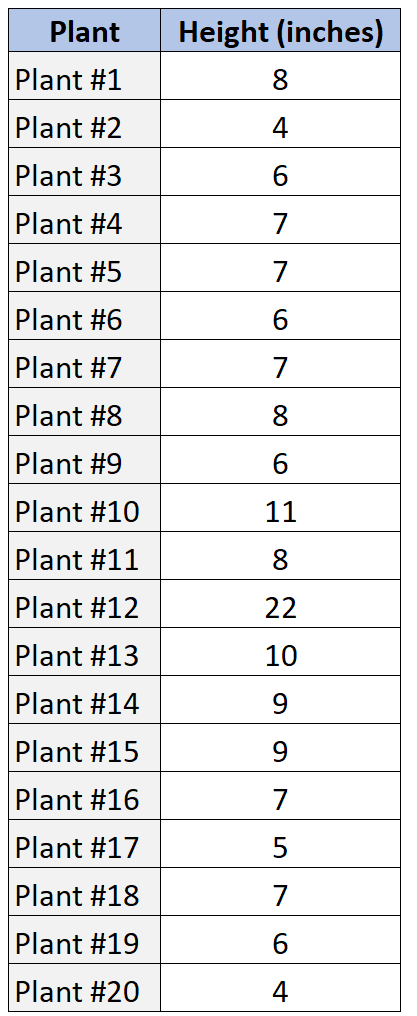
以下是我们如何使用 SOCS 来描述数据值的分布。
形状
首先,我们要描述分布的形状。
可视化分布形状的一个有用方法是创建直方图,它显示数据集中每个值的频率:
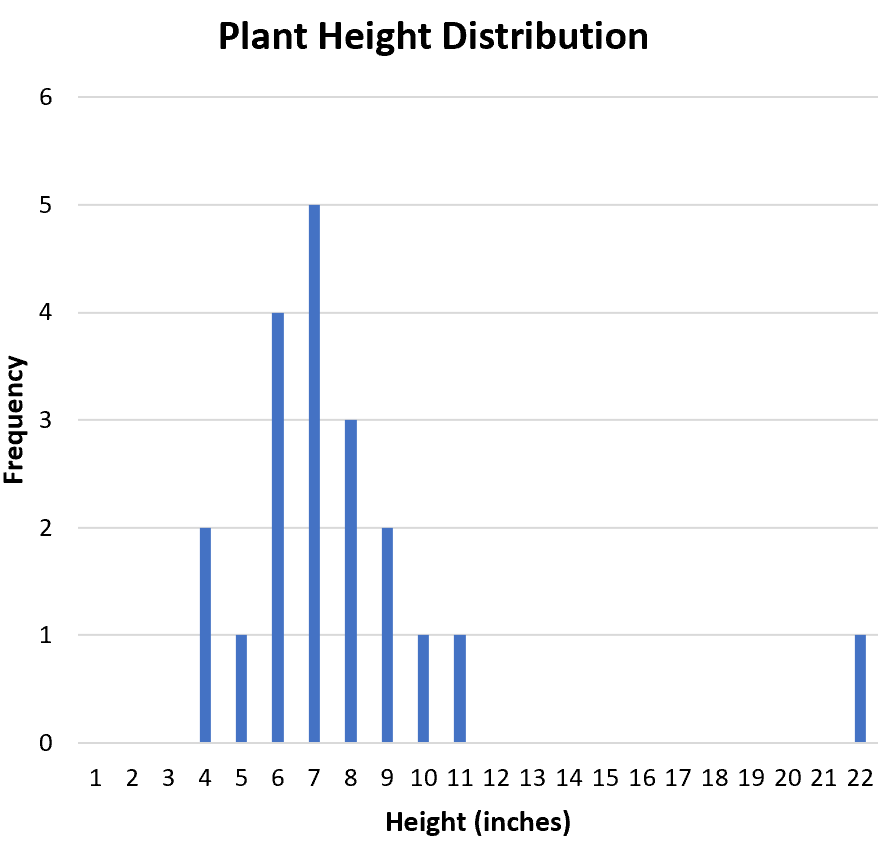
分布是对称的还是偏向一侧? 从直方图中我们可以看出,分布近似对称。换句话说,价值观并没有偏向某一方面。
分布是单峰(一个峰)还是双峰(两个峰)?分布是单峰的。它在值“7”处有一个峰值。
异常值
接下来,我们要确定数据集中是否存在异常值。从直方图中,我们可以直观地检查分布并发现 22 可能是异常值:
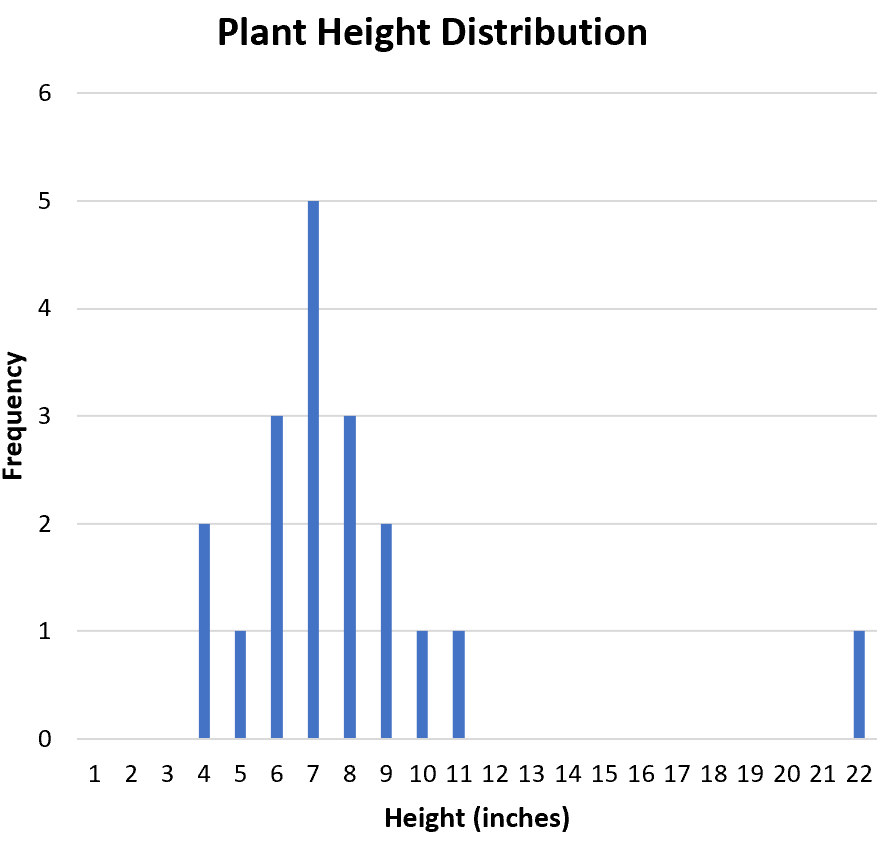
正式定义异常值的常用方法是任何高于第三个四分位数或低于第一个四分位数的四分位间距 1.5 倍的值。
使用四分位距计算器,我们可以输入20个原始数据值,看到第三个四分位数是9 ,四分位距是3 ,因此任何大于 9 + (1.5*3) = 13.5的值都是异常值,根据定义。
由于 22 大于 13.5,我们可以声明 22 为异常值。
中心
然后我们想要描述分布的中心位于哪里。我们可以使用的三种 常见的集中趋势度量是均值、中位数和众数。
平均值:这是分布的平均值。我们通过将所有单独的值相加然后除以值的总数来找到这一点:
平均值 = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7.85
中位数:这是分布的“平均”值。我们通过将所有值从小到大排序然后确定中值来找到这一点。结果是7 。
4, 4, 5, 6, 6, 6, 6, 7, 7, 7, 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22
众数:这是出现最频繁的值。结果是7 。
传播
接下来,我们要描述分布中数值的分布情况。我们可以使用的四种常见的离散度度量是极差、四分位数极差、标准差和方差。
极差:这是数据集中的最大值和最小值之间的差。结果是 22 – 4 = 18 。
四分位数范围:测量数据值中间 50% 的宽度。将 20 个原始数据值输入四分位数范围计算器,我们可以看到这等于3 。
标准差:这是数据值平均分布的度量。将20个原始数据值输入方差和标准差计算器,我们可以看到标准差等于3.69 。
方差:这只是标准差的平方。这等于 3.69 2 = 13.63 。
结论
以SOCS为指导,我们能够将植物高度分布描述如下:
- 该分布是单峰且对称的,这意味着它只有一个峰并且不偏向一侧或另一侧。
- 该分布有一个异常值:22。
- 该分布的平均值为 7.85,中位数为 7,众数为 7。
- 该分布的极差为 18,四分位距为 3,标准差为 3.69,方差为 13.63。
请注意,我们可以使用 SOCS 来描述任何分布,这对于我们充分了解分布的形状、是否有异常值、中心大约在哪里以及如何分布值数据来说是一个有用的方法。是。