莫兰的自我是什么? (定义&;示例)
Moran’s I是一种测量空间自相关的方法。
简单来说,它是一种量化值在 2D 空间中聚集程度的方法。它通常用于地理学和地理信息科学 (GIS)中,以衡量地图上不同特征的分组程度,例如家庭收入、教育水平等。
莫兰 I:公式
Moran’s I 的计算公式为:
I = (N/W)*ΣΣw ij ( xi – x )(x j – x )/Σ( xi – x ) 2
金子:
- N:由i和j索引的空间单元的数量
- W:所有 w ij的总和
- x:感兴趣的变量(家庭收入、受教育年限等)
- x : x 的平均值
- w ij :空间权重矩阵
您可能永远不需要手动计算此测量值,因为大多数统计软件都可以为您计算它,但了解幕后使用的公式会有所帮助。
Moran’s I 的值范围为 -1 到 1,其中:
- -1:感兴趣的变量完全分散
- 0:感兴趣的变量是随机分散的
- 1:感兴趣的变量完美分组
除了计算 Moran’s I 之外,大多数统计软件还会计算相应的 p 值,该值可用于确定数据是否随机分散。
莫兰检验使用以下原假设和备择假设:
原假设 (H 0 ):数据随机分散。
备择假设 ( HA ):数据不是随机分散的,也就是说,它以可见的模式分组。
如果与 Moran’s I 对应的 p 值低于一定的显着性水平(即 α = 0.05),那么我们可以拒绝零假设并得出结论:数据在空间上聚类,因此它们不太可能在空间上聚类。偶然发生的。
莫兰 I:一些例子
以下示例代表 Moran’s I 具有不同值的假牌。
假设地图上的每个方块代表一个县,平均家庭收入超过 50,000 美元的县显示为蓝色。
Moran’s I = 0:平均家庭收入是随机分散的(即随机区域中的随机集群)。
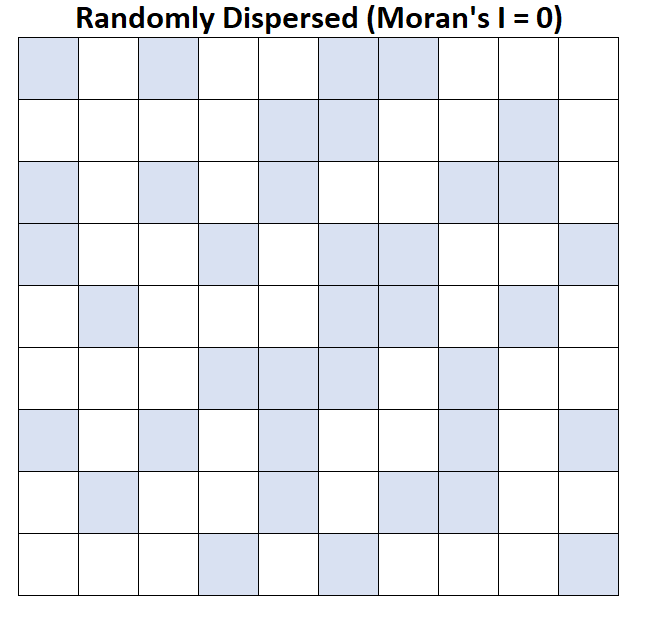
Moran’s I = -1:平均家庭收入完全分散。
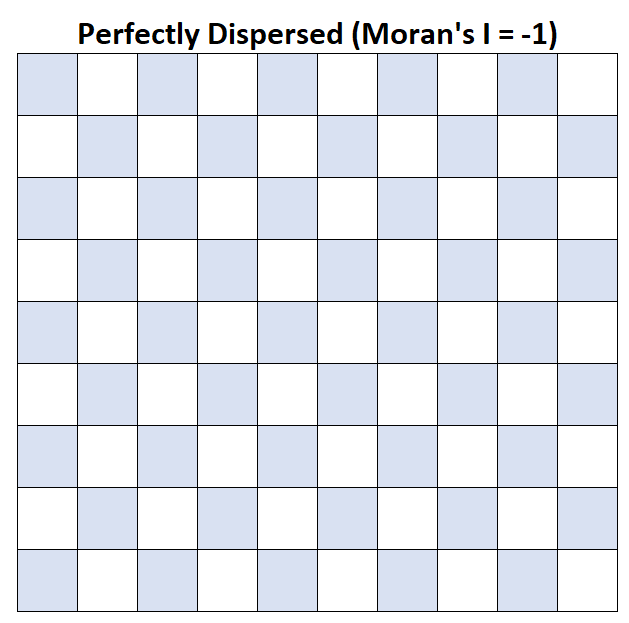
Moran’s I = 1:平均家庭收入完全分组。
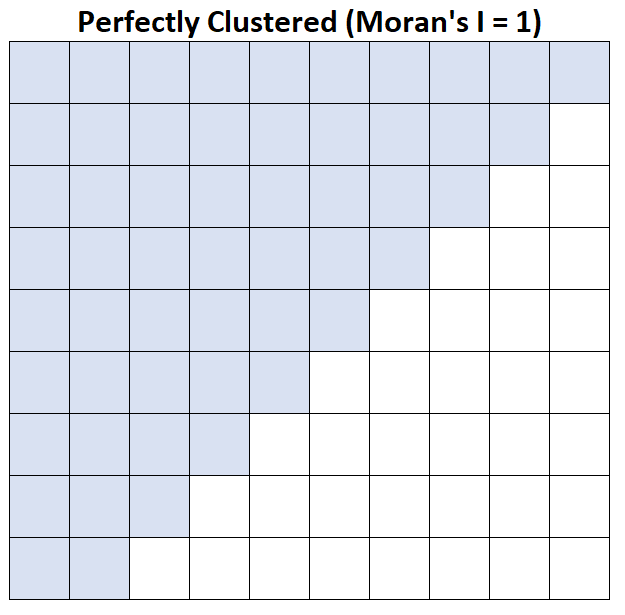
在统计软件R中计算Moran’s I的具体例子请参考本例。