效应大小:它是什么以及为什么重要
“统计显着性是结果中最不有趣的事情。你需要用量级来描述结果——治疗不仅会影响人们,而且会影响他们的程度。 -吉恩·V·格拉斯
在统计学中,我们经常使用p值来确定两组之间是否存在统计显着差异。
例如,假设我们想知道两种不同的学习方法是否会导致不同的测试分数。因此,我们有一组 20 名学生使用一种学习技巧来准备测试,而另一组 20 名学生则使用不同的学习技巧。然后我们给每个学生进行相同的测试。
运行两个样本 t 检验以确定均值差异后,我们发现检验的 p 值为 0.001。如果我们使用0.05的显着性水平,这意味着两组的平均结果之间存在统计学上的显着差异。因此,学习技巧对测试结果有影响。
然而,虽然 p 值告诉我们学习技术对考试成绩有影响,但它并没有告诉我们这种影响的大小。为了理解这一点,我们需要知道效应大小。
什么是效应量?
效应大小是量化两组之间差异的一种方法。
虽然 p 值可以告诉我们两组之间是否存在统计上的显着差异,但效应大小可以告诉我们这种差异到底有多大。在实践中,效应大小比 p 值更有趣、更有用。
有三种方法可以衡量效应大小,具体取决于您正在进行的分析类型:
1.标准化均差
当您想要研究两组之间的平均差时,计算效应大小的适当方法是使用标准化平均差。最常用的公式称为 Cohen’s d ,其计算如下:
科恩D = ( x1 – x2 )/ s
其中x 1和x 2分别是第 1 组和第 2 组的样本均值, s是抽取这两个组的总体的标准差。
使用这个公式,效应大小很容易解释:
- d为 1 表示两组的平均值相差一个标准差。
- d为 2 表示组平均值相差两个标准差。
- d为 2.5 表示两个平均值相差 2.5 个标准差,依此类推。
另一种解释效应大小的方法是:效应大小为 0.3 意味着第 2组中的平均得分比第 1组中的平均得分高出 0.3 个标准差,因此超过了第 1组中得分的 62%。 。
下表显示了不同的效应大小及其相应的百分位数:
| 规模效应 | 第2组中低于第1组人员平均水平的百分比 |
|---|---|
| 0.0 | 50% |
| 0.2 | 58% |
| 0.4 | 66% |
| 0.6 | 73% |
| 0.8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99.9% |
效应量越大,每组中平均个体之间的差异就越大。
一般来说,0.2 或更小的d被认为是小效应量,0.5 左右的d被认为是中等效应量,而 0.8 或更大的d被认为是大效应量。
因此,如果两组的均值相差不至少 0.2 个标准差,则即使 p 值具有统计显着性,差异也不显着。
2.相关系数
当要研究两个变量之间的定量关系时,计算效应大小的最常见方法是使用皮尔逊相关系数。它是两个变量X和Y之间线性关联的度量。它的值介于 -1 和 1 之间,其中:
- -1 表示两个变量之间完全负线性相关
- 0 表示两个变量之间不存在线性相关
- 1 表示两个变量之间存在完全正线性相关
皮尔逊相关系数的计算公式相当复杂,有兴趣的可以在这里找到。
相关系数离零越远,两个变量之间的线性关系越强。这也可以通过创建变量X和Y的值的简单散点图来看出。
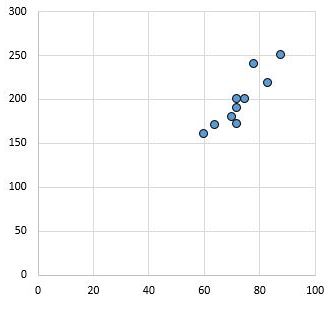
例如,下面的散点图显示了相关系数为r = 0.94 的两个变量的值。
该值远非零,表明两个变量之间存在很强的正相关关系。
相反,下面的散点图显示了相关系数为r = 0.03 的两个变量的值。该值接近于零,表明两个变量之间实际上不存在关系。
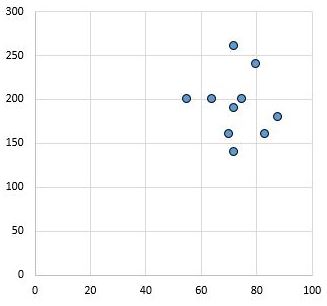
一般来说,如果皮尔逊相关系数r的值约为 0.1,则认为效应大小较小;如果r约为 0.3,则认为效应大小为中等;如果r等于或大于 0.5,则认为效应大小较大。
3.优势比
当您想要研究治疗组的成功几率与对照组的成功几率时,计算效应大小的最常见方法是使用优势比。
例如,假设我们有下表:
| 规模效应 | #成功 | #棋 |
|---|---|---|
| 治疗组 | 有 | 乙 |
| 控制组 | VS | D |
优势比计算如下:
优势比 = (AD) / (BC)
优势比距离 1 越远,治疗产生实际效果的概率就越高。
使用效应量而非 P 值的好处
与 p 值相比,效应大小有几个优点:
1.效应大小可以帮助我们更好地了解两组之间的差异有多大或者两组之间的关联有多强。 p 值只能告诉我们是否存在显着差异或显着关联。
2.与 p 值不同,效应量可用于定量比较在不同环境下进行的不同研究的结果。因此,荟萃分析中经常使用效应量。
3. P值会受到大样本量的影响。样本量越大,假设检验的统计功效就越大,使其能够检测到甚至很小的影响。尽管效应量较小且可能没有实际意义,但这可能会导致 p 值较低。
一个简单的例子可以清楚地说明这一点:假设我们想知道两种学习方法是否会导致不同的测试分数。我们有一组 20 名学生使用一种学习技巧,而另一组 20 名学生使用不同的学习技巧。然后我们给每个学生进行相同的测试。
第1组平均分为90.65 ,第2组平均分为90.75 。样本 1 的标准差为2.77 ,样本 2 的标准差为2.78 。
当我们执行独立的双样本 t 检验时,结果表明检验统计量为-0.113 ,相应的 p 值为0.91 。平均测试成绩之间的差异不具有统计显着性。
但是,考虑两个样本的样本量均为200 ,但平均值和标准差保持完全相同。
在这种情况下,独立的双样本 t 检验将显示检验统计量为-1.97且相应的 p 值略低于0.05 。平均测试成绩之间的差异具有统计显着性。
大样本量可以得出统计显着性结论的根本原因是用于计算t检验统计量的公式:
检验统计量t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
请注意,当 n 1和 n 2较小时, t检验统计量的整数分母较小。当你除以一个小数时,你会得到一个大数。这意味着t检验统计量会很大,相应的 p 值会很小,从而导致统计显着的结果。
什么被认为是良好的效应量?
学生经常问的一个问题是:什么被认为是好的效果大小?
简而言之:效应大小不能是“好”或“坏”,因为它只是衡量两组之间差异的大小或两组之间关联的强度。
然而,我们可以使用以下经验法则来量化影响的大小是小、中还是大:
科恩的D:
- 0.2 或更小的d被认为是较小的效应量。
- 0.5 的d被认为是中等效应大小。
- 0.8 或更大的d被认为是较大的效应量。
皮尔逊相关系数
- r的绝对值在 0.1 左右被认为是较小的效应量。
- r的绝对值在 0.3 左右被认为是中等效应大小。
- r的绝对值大于 0.5 被认为是较大的效应量。
然而,“强”相关性的定义因领域而异。请参阅本文以更好地了解不同行业之间的强相关性。